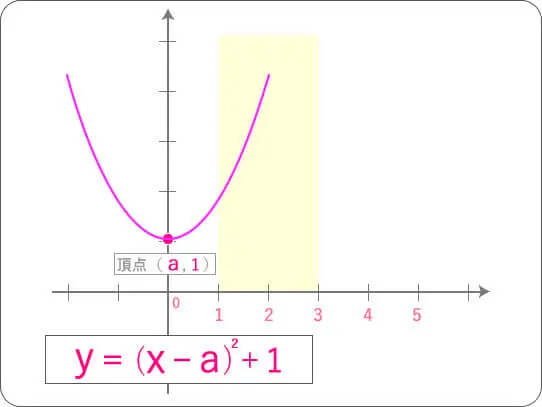
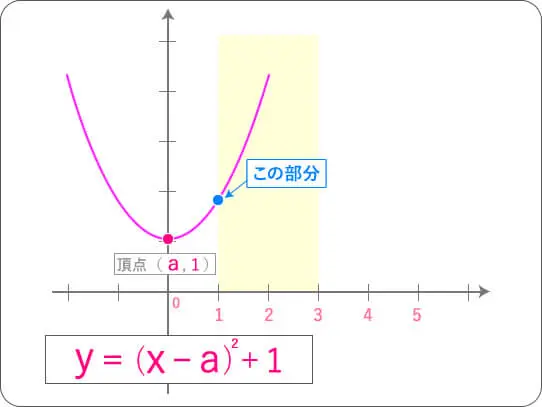
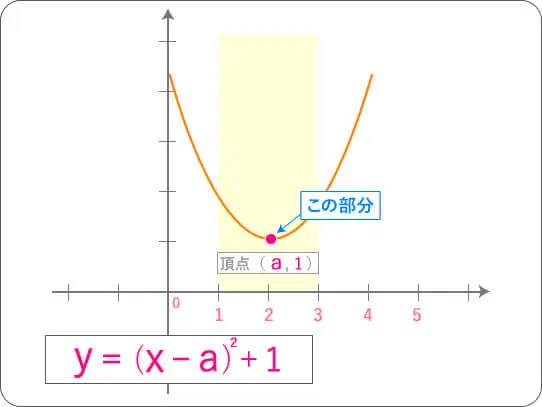
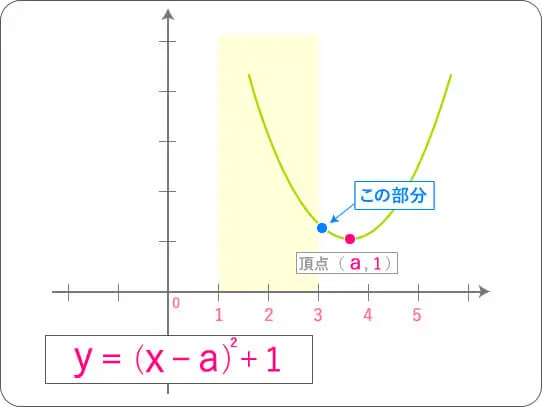
日時間分秒


はじめに
看護大学の受験を考えている皆様。
看護大学に通うことで、看護師や保健師・助産師になれます。
さらには世界的に活躍できる国際看護師になれるという夢もあります。
しかし、誰でも看護大学に合格できるわけではありません。
この記事では、これから看護大学の受験を考えている皆様が
どうすれば看護大学に合格できるのか
看護大学に通えばどんなメリットがあるのか
看護大学を卒業すればどんなことが待っているのか
気になることをピックアップして書いていきたいと思います。
ぜひ参考にして、看護大学の合格に一歩でも近づいてください。
1. 看護大学に入るまでの基礎知識

まず看護大学を受験するにも最低限の条件があります。
その1つとして中卒では看護大学を受験することはできません。
看護大学の受験が出来る人は
高校卒業資格を取得している者
高等学校を卒業した者と同等以上の学力があると認められる者
受験年度の3月に卒業の見込みがある者
に限られます。
詳しくは各看護大学の募集要項を見る必要もあります。
しかし、上記の条件を満たしている方は看護大学の受験資格があると思っていいでしょう。
1.1 看護大学とは?

看護大学(かんごだいがく)とは、通常の大学と同様に4年間、看護の教育を行っている大学のことを言います。
かつては、看護大学のカリキュラムを修了した者は卒業と同時に
「看護国家試験受験資格」と「保健師国家試験受験資格」の両方を取得できましたが、
近年、看護大学の増加と同時に保健師の養成課程を選択制としている看護大学も増えています。
これから保健師になりたくて看護大学を受験する方は、
保健師養成課程が必須なのか!?選択制なのか!?
見ておくのもいいかもしれません。
看護大学を経て、
保健師になるにも・助産師になるにも
必ず看護国家資格取得が必須なので看護大学で、「保健師」や「助産師」を目指している人は
看護大学で看護国家試験受験資格の取得をしておきたいところです。
1.2 看護大学に入るまでの手順

看護大学に入学するにもいくつかの方法があります。
指定校推薦入試
公募入試
社会人入試
AO入試
一般入試
この5種類があります。
この5種類の試験の中で、看護大学側が課する条件をクリアできれば無事、
看護大学生として入学することが出来ます。
入試方法によっては同じ看護大学だったとしても、
入試日程が異なったり、その度受ける試験によって条件があるので、
どの入試も好き放題受験できるわけではありません。
受験しようと思っている看護大学のHPや募集要項は、常に確認しておくことをお勧めします。
1.3 看護大学に入学するメリット

H30年度の時点で看護大学は全国に263大学あります。
もちろんこれからもまだまだ増えていくでしょう。
その背景には、看護大学を受験する学生が増加しているからです。

このように看護系の学校へ入学する学生が年間約67,000人。
看護大学に入学するものが、約23,000人となっています。
これは、看護師になる3人に1人が看護大学卒業生となります。
看護大学に入学するメリットとしては、技術的なことはもちろん、医療が高度になってくる中で
学術的な知識を身につけたい人が看護大学を選択します。
看護大学を目指す人の多くが「高校生」と「浪人生」です。
また少数ではありますが、「社会人」も数人受け入れて貰えます。
看護大学のメリット
・4年制だから余裕をもって学べる
・他の大学と同じく一般教養も学べる
・在学中に保健師や助産師への道が開かれる
・大学生としてのキャンパスライフを楽しめる
・大学卒は給料が高めに設定されている
などが挙げられます。
1.4 看護大学に入学するデメリット
メリットをみると看護大学に入学したいと思う人もいるかもしれませんが、誰もが看護大学を選択するわけではありません。
「やっぱり私は看護専門学校の方がいい。」
このように話す人も少なくありません。
その理由は、看護大学へ入学して看護師になるまでには少なくとも4年間が必要となります。
看護大学を選択した場合には、皆様が4回生になった時看護専門学校卒の人はすでに勤務していることになります。
この1年間は今後仕事をする中では大きな差となります。
また、看護専門学校は看護大学とは異なり、常に病院実習で技術を磨いていきます。
なので、看護大学卒の学生よりも技術に関しては数段上とも言われています。
そして、看護専門学校卒の方は同系列の病院で働くことが多いので、看護大学卒の方はアウェイ感を感じることもあります。
この部分が看護大学へのデメリットになります。
看護大学のデメリット
・看護師になるまでに4年間かかる。
・実習技術が専門学校卒の人より劣る
・就活がある
・専門学校と比べ学費が高い。
1.5 看護大学にかかる学費

看護大学に通うというだけで少しブランド感もあり、
学費が高いんじゃないのかなぁ・・・
そう思う学生もたくさんいます。
そこで、気になる看護大学の学費を説明していきます。
実際、看護師になるには
看護専門学校
看護短大
看護大学
この3種類がありましたね。
この中で一番学費が安いのは「看護専門学校」になります。
その次に安いのが「国立の看護大学」なのですが、学費が安いだけではなく偏差値も高いので、
合格することが非常に難しくもあります。
最後に、学費が一番高いのが、「私立の看護大学」になります。
私立の看護大学でもそれぞれ学費には差があり、
安いところで約1,150,000円
高いところでは約2,500,000万円
と100万円近くの差があります。
1.6 看護大学で入学金と授業料以外にかかる費用。
一般的に大学に通うとなれば、「入学金」と「授業料」が必要。
このイメージがあると思いますが、看護大学の場合は少し異なります。
看護大学では、勉強を学ぶ+実習ということもあり、
「入学金」と「授業料」以外に必要なコストがあります。
施設整備費
教育充実費
教材費
テキスト購入費
白衣代
制服代(制服が必要な学校)
学生保険料
等が「入学金」と「授業料」以外に必要となります。
これらの費用も看護大学により様々で、
看護大学へ受験する前には、前もって確認しておきたいところです。
国立の看護大学を一例に挙げてみると

いくら入学金と授業料が安いからといっても
看護大学は医療系の大学なので、その他の費用が掛かってくることを想定しておきましょう。
1.7 看護大学と看護専門学校の違い

看護大学を受験しようと考えている人の中には、
看護専門学校と看護大学
実際にはどちらの方がいいんだろう!?
このように疑問を持つ人も多いかもしれません。
看護師になるだけを考えれば、3年で修了できる看護専門学校がお勧めです。
しかし、看護師だけではなく将来、専門看護師になることを考えているのであれば、
大学院に進む必要があるので、看護大学に行く必要があります。
1.8 看護大学と看護大学校の違い
看護大学と看護大学校では所割が異なります。
看護大学は文部科学省の所管
看護大学校・看護専門学校は厚生労働省の所管
看護大学校も、看護大学と同様に、
4年間学校で学び、「高度専門士」の称号が付与された者は
大学卒業した者と同等の学力があると認めれられ
大学院の入学資格を取得することができます。
学校での授業内容(看護に関して)は、『保健師助産師看護師法』で決められているため
看護大学でも看護大学校でも学ぶ内容は同じです。
2. 看護大学の受験に合格するためには

これから看護大学を目指す「高校生」「浪人生」「社会人」の皆様にとって、
どうすれば看護大学に合格できるのか!?
一番気になるところですよね。
看護大学を受験するにも
指定校推薦入試
公募入試
社会人入試
AO入試
一般入試
5つの受験方式があります。
それぞれ受験方式には条件があり、満たしてなければテストに参加できない場合もあります。
どの入試方式を利用するのかも早い時期から考えておくと看護大学の受験までスムーズにことが進みます。
2.1 看護大学の受験に合格するには指定校推薦使おう。
指定校推薦入試という言葉を一度は聞いたことがあるかもしれません。
指定校推薦とは高校生の皆様が、高校3年間継続して学校内で行われるテストで
好成績を残した方にだけに与えられる特別な推薦枠のことを言います。
指定校推薦枠を勝ちとれば、
志望する看護大学と「面接」or「小論文」のテストだけで合格することができます。
一見羨ましそうに思われる推薦枠ですが、
この推薦枠を勝ち取るためには高校入学時から継続した努力が必要で
尚且つ結果も求められるので大変ではあります。
しかし、指定校推薦枠を勝ち得た学生は一般的な試験を受けなくても
看護大学側から優秀な学生と認めて貰えます。
指定校推薦のメリット
・定期テストだけに照準を絞れる。
・圧迫面接にはならない。
・指定校推薦枠で落ちることは滅多にない
指定校推薦のデメリット
・合格すれば必ず入学しなければならない
・早めに試験が終わるのでモチベーションが下がる
・看護大学によっては入学前に課題ある
指定校推薦で看護大学に合格する場合の注意点は、合格すれば必ず入学しなければならないところです。
その理由は、あなたが通う高校側と看護大学側との信頼関係で成り立っているシステムです。
もし仮に、
看護大学に合格したのに入学を拒否。
看護大学入学後の素行に問題があった場合。
には、看護大学側から指定校推薦枠の見直し等になるで注意しましょう。
2.2 看護大学に合格するには公募入試を使おう。

看護大学には、高校生が受験しやすいように公募入試があります。
公募入試とは高校3年間で、看護大学が設定する一定の条件(評定平均)を
クリアした高校生に受験資格が与えられます。
但し、一定の条件をクリアした学生が受験するので、
近年、看護師を目指す人が増加しているので、一般入試よりも合格しにくい傾向があります。
万が一、第一志望の看護大学を公募入試で不合格になったとしても
一般入試で再度受験することは可能なので、
第一志望の看護大学を受験する機会が増えることになります。
公募推薦入試のメリット
・高校で習う基礎学力を中心に作られています。
・評定平均値がプラスされる。
・熱意を伝えれる。
公募推薦入試のデメリット
・看護大学に合格すれば必ず入学
・学力だけでは決まらない
・併願が難しい
看護大学の公募推薦入試にはこのようなメリット・デメリットがあります。
2.3 看護大学に合格するにはao入試使おう。
そもそもAO入試って何なの!?公募入試と何が違うの!?
そう思われている方もたくさんいると思います。
この大きな違いは、
推薦入試=学校が生徒を推薦する
AO入試は=自らが立候補する
このような形になっています。
まず初めに、AO入試で合格するには、調査書や自己アピールに優れていなければなりません。
看護大学側が指定する評定平均がクリアできず、受験の機会を持ちたいと思う学生がAO入試を選択する場合もありますが、
活動実績の評価が低い場合
高校生活での評定が低い場合
こういった場合は、看護大学に合格することは難しくなります。
誰でも受験できるだけに、これで看護大学に合格しやすのではと思われがちですが、
書類審査が厳しく合格することが難しいとされています。
逆に、学生時代に多くの実績がある場合にはAO入試を受験すれば合格できる確率は高いです。
2.4 看護大学に合格するには社会人入試を使おう。
社会人にとって、年齢が立てば立つほど
もう一度大学へ通うことに対して腰が重くなりますよね。
でも、そんな社会人の皆様が少しでも受験しやすいように、
社会人入試を設けている看護大学があります。
もちろん入学後には、自分自身よりも年齢の低い学生と
一緒に学ぶことになりますが、社会人入試を利用することで、
社会人の皆様が看護大学へ受験するチャンスが
一般試験と含め2度あることになります。
社会人の皆様が看護大学の受験を考えた時には、
・社会人入試がある看護大学なのか?
・社会人入試がない看護大学なのか!?
は調べておきたいところですね。
看護大学の社会人入試は狭き狭き門ではありますが、
大学を経てから看護師になりたい人にはお勧めです。
2.5 看護大学に合格するには一般入試を使おう。
看護大学を受験する人が一番多く使うテストが一般入試になります。
一般入試では
「高校生」
「浪人生」
「社会人」
とありとあらゆる学生が看護大学を受験します。
また受験生が増加することで看護大学へ合格するための倍率が跳ね上がります。
一般入試の魅力は何といっても看護系なのに面接がないところです。
看護専門学校では公募入試・社会人入試・一般入試とどの入試形式でも面接試験があるだけに、
高校生でも社会人でも面接の苦手な人にとってが嬉しいテストです。
看護系の学校に行きたいけど面接が苦手な人にとっては1つの方法になるでしょう。
看護 予備校 KAZアカデミーが作成。看護受験に役に立つ学習一覧