2次関数 : 軸に文字を含む場合の最大値と最小値②
「高校数学：文字のグラフの範囲に注意の巻」vol.20

前回は文字が含まれている放物線は

右に左にとフラフラしていることを学びましたね。

もう一度グラフの動きを見ておきましょう。

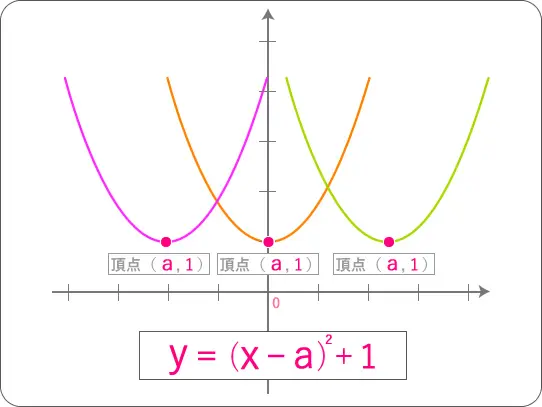
このような式の場合、解っていることは、

「放物線の向き」と「y = １」そして軸が「X ＝ a」

でしたよね。

そこで今回は、このグラフに

範囲が決められている場合どのような動きになるのか！？

それを勉強していきます。

範囲ごとに放物線の値を求めよう。

この問題は、

(1≦x≦3)の間であれば最小値はどうなるのか！？

それを聞いていますよね。

それでは、まず一番左端にある紫色の放物線の場合

どのようになるのかを説明します。

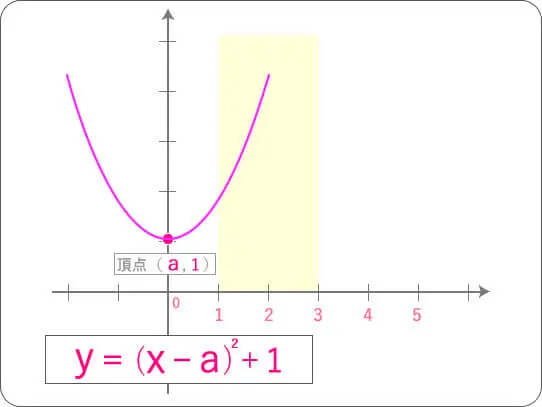
聞かれている(1≦x≦3)の範囲に薄く色を塗っておきますね。

とその前に、

軸はどこでしたか！？

そうです。

X＝a

でしたよね。

これは常に意識しておいて下さい。

それでは、この紫色の放物線の最小値の場所を探してみましょう。

わかりますか！？

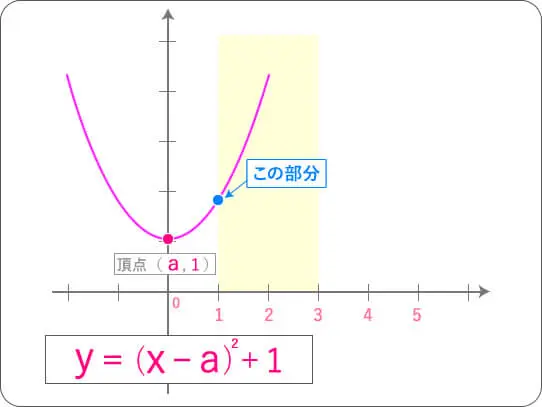
この青色の点の部分ですよね。

よく勘違いするのが、

最小値or最大値　＝　頂点

と思ってしまう人もいますが、

それは範囲が指定されていない場合です。

なので、今回のこの紫の放物線の最小値は、

このようになります。

X＝1の時、軸のaが常に1よりも小さいが大切です。

では次にオレンジ色の放物線のことを考えてみましょう。

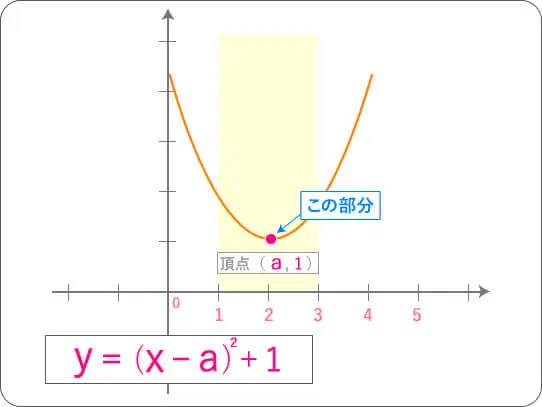
どうやら、このオレンジ色の放物線の場合、

(1≦x≦3)の間であれば頂点が最小値のようです。

なので、

1≦x≦3の時は軸は常にX＝aになりことが重要です。

最後に、緑色の放物線を見てみましょう。

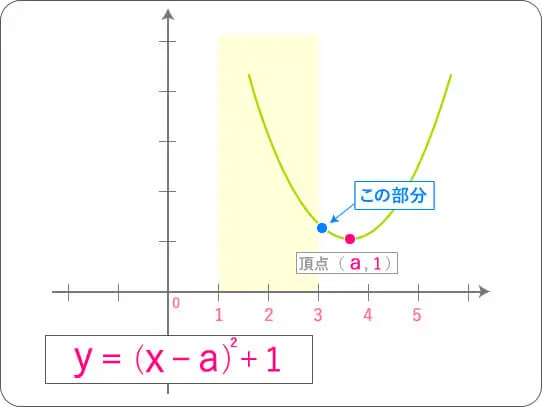
どうやら、この緑色の放物線の場合、

X＝3の時、が最小のようです。

なので、

このようになります。

X＝3の時、軸のaは常に3よりも大きいことを理解することが大切です。

つまり、

この2次関数の問題の場合は、

３つの答えを書かなければなりません。

これを場合分けと言います。

場合によって答えを分けて下さいね。って感じですよね。

ちょっと難しかったですよね。

この問題は看護受験生の大きな壁となる部分でもあります。

これがしっかりと理解できた時には、

2次関数で理解できない問題はないでしょう。

• «Q19.軸に文字を含む場合の最大値と最小値①
• Q21.軸に文字を含む場合の最大値と最小値③»