2次関数 : 定義域・値域（１）
「関数で悩ますグラフの範囲の巻」vol.4

週末はいかがお過ごしでしたか？

本日から

いよいよ新年度が始まりますね。

入学式の終えた学生様も

ご報告有難うございました。

来年は、

あなたの番ですよね。

でも、焦りは禁物なので、

忙しい中受験勉強に励んでいる受験生の皆様は、

くれぐれも体調には気を付けてくださいね。

それでは、

本日も二次関数のお勉強をしていきます。

前回は、グラフの書き方の説明をしましたが、

今回は、グラフの範囲についての勉強をします。

関数の定義域・値域って何？

皆さんは、

「定義域」や「値域」という言葉

を聞いたことはありますか？

日常では使わない言葉ですよね。

簡単に言うと

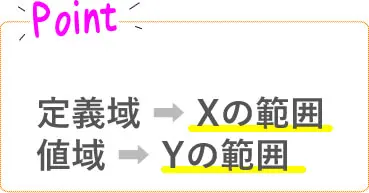
を表します。

言葉だけだとややこしいと思うので、

問題を解いてみましょう。

まずは（1）のグラフから書いてみたいと思います。

前回、同様一次関数のグラフは

１つ目の点：切片をとること。
２つ目の点：分数にすること。

でしたよね。

では、グラフ書きます。

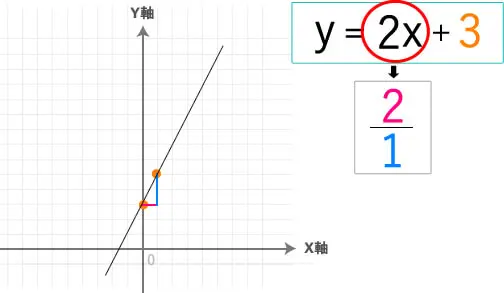
ここまでは、前回の復習になります。

でもここで一つ、

重要なことがあります。

それは、今回の問題は

自由にグラフを書くのではなく

このように範囲が決まってるということです。

なので、その範囲だけを

実線にしてあげます。

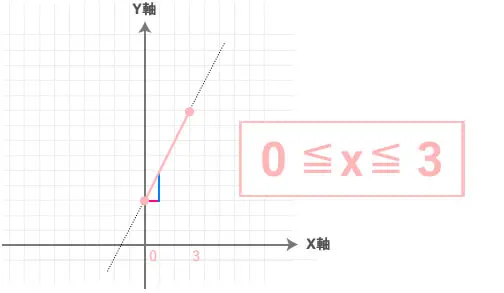
どうですか？

できましたか？

しかし、

もし仮に、点の位置がわからない場合は、

Ｘ=０とＸ=３を

この直線の式のＸに代入します。

すると、

と求めることもできるので、

確実に点を取りたい時には代入

を使いましょう。

それでは、

（２）の値域を求めてみましょう。

値域というのは何でしたか？

Ｙの範囲でしたよね。

それではもう一度グラフを見てみましょう。

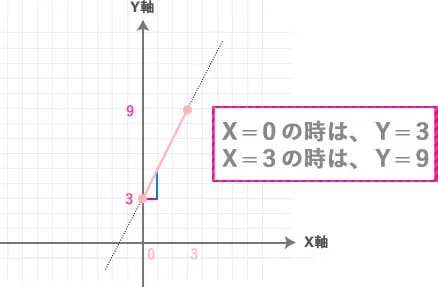
これを見るとＸの範囲が

0≦X≦3の時

Ｙはどこからどこまでになっていますか？

そうです。

3から9の間になっていますよね！？

これがＹの値域になります。

なので、答えは、

今回は、1次関数が基本となるので、

1次関数を使って、

定義域と値域の説明をしましたが、

次回は、いよいよ2次関数を使って範囲を勉強していきます。

• «Q3.グラフを書き方
• Q5.定義域・値域（2）»