2次関数 : グラフの見分け方！！
「グラフの違いはこれでわかる巻」vol.2

皆さんは、「関数」という言葉を

聞いただけで

「えっ・・・難しそう」

なんて抵抗はありませんか？

関数には

「1次関数」「2次関数」「3次関数」など

いくつかの種類があるのですが

看護受験に必要な関数は

「1次関数」と「2次関数」

だけです。

言葉だけでは難しいので

「1次関数」と「2次関数」のグラフを見てみましょう。

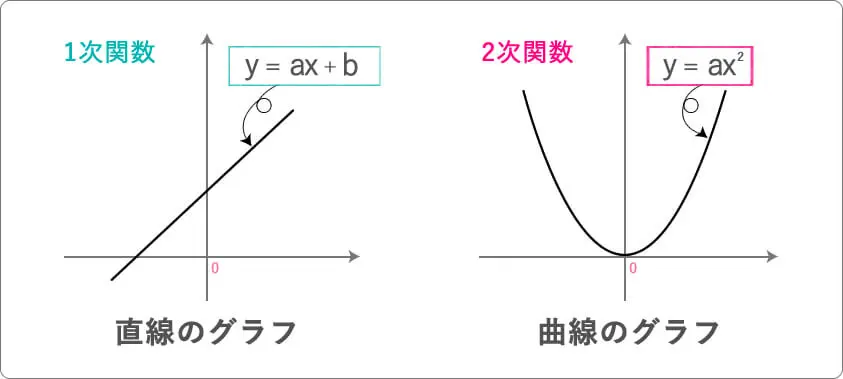
このように見ると

「1次関数」と「2次関数」

とでは、全く違いますよね。

でも

なぜこのようなグラフの差がでるのか！？

それは、出題されている問題により

式が異なってくるから

です。

するとどうなるでしょうか？

こんな式が出来上がりませんか？

ですよね。なので、

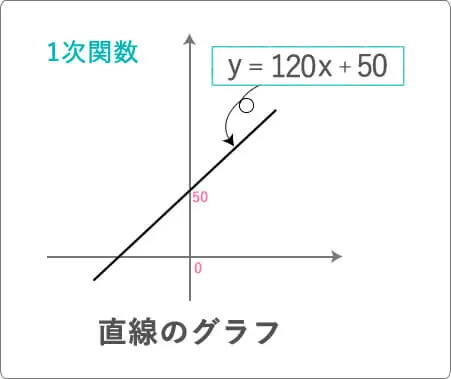
この場合は、一次関数と見なされます。

では、次にこのような文章題があったとします。

するとどうなるでしょうか？

こんな式が出来上がりませんか？

ちなみに円の面積の求め方は

半径×半径×円周率（3.14）

なので、覚えておいてくださいね。

なので、

グラフに表してみると、

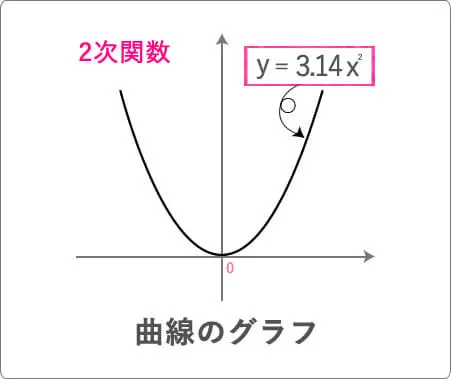
なので、これは2次関数になります。

なんとなく

グラフの使い分けはわかりましたか？

大切なことは、式を書くだけではなく

式ができれば、

グラフに書いてみることも重要です。

1次関数は直線
2次関数は曲線

これを覚えておきましょう。

• «Q1.2次関数とは
• Q3.グラフを書き方»