2.看護学校が面接で気になるニュースを聞く目的。
そもそも、なぜ看護学校の受験で
最近気になるニュースについて聞くのか!?
受験生によっては、
個人的なことを聞いてもらえた方が
もっとアピールができるんだけど・・・
なんて思ってしまいがちですが、
実は、
「最近気になるニュース」と質問するだけで
あなたの日常生活の一部が垣間見えます。
もくじ
- 1.看護学校の受験面接で気になるニュースを聞かれたらどうする!?
- 1.1「あなたが最近気になっているニュース」で選ぶべき種類。
- 1.2「なぜそのニュースに興味を持ったのですか?」聞かれる理由。
- 2.看護学校が面接で気になるニュースを聞く目的。
- 2.1看護受験生が日頃から情報収集する習慣があるか。
- 2.2ニュースに対して受験生が自分の考えを持っているのか。
- 2.3数あるニュースの中からどれを選ぶべきか。
- 3.看護学校が面接で「気になるニュース」を伝える文章の組み立て
- 3.1相手に伝える時の文の構成には要注意。
- 3.2気になるニュースの気になる部分をピックアップ。
- 3.3何度も読んで相手に伝わるか最終チェック。
2.1 看護受験生が日頃から情報収集する習慣があるか
ここで皆さんに質問です。
筆記テストで高得点なんじゃないの!?
確かに、筆記テストで高得点とることも大切ですが、
それだけではありません。
実際、看護学校側に話を聞いたところ、
勉強ができるだけでは看護師としてちょっと・・・
との話もあります。
看護師になれば、患者さんやご家族と話す機会も増えます。
患者さんは毎日、
「雑誌や新聞」の内容から看護師に話しかけることも多々あります。
患者様が看護師とコミュニケーションをとろうとしているにも関わらず
看護師から返答が出来なければ、
患者さんがその看護師に心を閉ざす恐れもあります。
こういった背景も含め、
看護受験では「筆記勉強」だけではなく普段から新聞や雑誌などを読み、
あなたが偏った知識の人間でないかを見ています。
2.2 ニュースに対して受験生が自分の考えを持っているのか。
最近気になるニュースを聞く理由として、
ニュースを知っているだけではなく、
そのニュースに対して
あなたがどんな考え方を持っているのか
が重要なポイントです。
例えば、とあるニュースで動物殺傷事件があったとします。
「あなたはこれについてどう思いますか!?」
と看護学校の面接官に質問された場合、
どう答えますか?
仮に「私も動物は嫌いなので殺傷してもいいと思います。」
なんて答えれば、100%不合格になりますよね。
えっ
そんな回答をする人っているの!?
なんて思うかもしれませんが、
実際にいます。
確かに、個人的に動物が苦手な人もいるかもしれませんが、
どんな小さな虫でも殺めることは一般的に善しとされていません。
なので、ポイントとしては動物が殺傷されたことではなく
何故、動物殺傷至ったのか!?
その犯人の感情にポイントを持って話を考えた方が答えやすいでしょう。
2.3 数あるニュースの中からどれを選ぶべきか。
新聞や情報サイトを見ていると
毎日、異なったニュースが飛び交っています。看護学校の受験では、
この数あるニュースの中から1つもしくは2つ選ばなければなりません。
もちろんどんなニュースを選んだとしても
間違いではありませんが、
あなたをマイナスイメージにしてしまうニュースは
選ばない方がいいでしょう。
そこで、
できるだけ答えやすいニュースを選びたいのですが、
ただ答えやすいニュースを選んだ時には、
看護学校の面接時に、
他の受験生とかぶってしまう場合があります。
それを避けるためにも
最低2つは準備しておきたいところです。

看護学校の面接で気になるニュースまとめ
- 気になるニュースをピックアップ | 2025年11月版
- 気になるニュースをピックアップ | 2025年10月版
- 気になるニュースをピックアップ | 2025年9月版
- 気になるニュースをピックアップ | 2025年8月版
- 気になるニュースをピックアップ | 2025年7月版
- 気になるニュースをピックアップ | 2025年6月版
- 気になるニュースをピックアップ | 2025年5月版
- 気になるニュースをピックアップ | 2025年4月版
- 気になるニュースをピックアップ | 2025年3月版
- 気になるニュースをピックアップ | 2025年2月版
- 気になるニュースをピックアップ | 2025年1月版
- 気になるニュースをピックアップ | 2024年12月版
- 気になるニュースをピックアップ | 2024年11月版
- 気になるニュースをピックアップ | 2024年10月版
- 気になるニュースをピックアップ | 2024年9月版
- 気になるニュースをピックアップ | 2024年8月版
- 気になるニュースをピックアップ | 2024年7月版
- 気になるニュースをピックアップ | 2024年6月版
- 気になるニュースをピックアップ | 2024年5月版
- 気になるニュースをピックアップ | 2024年4月版
- 気になるニュースをピックアップ | 2024年3月版
- 気になるニュースをピックアップ | 2024年2月版
- 気になるニュースをピックアップ | 2024年1月版
- 気になるニュースをピックアップ | 2023年12月版
- 気になるニュースをピックアップ | 2023年11月版
- 気になるニュースをピックアップ | 2023年10月版
- 気になるニュースをピックアップ | 2023年9月版
- 気になるニュースをピックアップ | 2023年8月版
- 気になるニュースをピックアップ | 2023年7月版
- 気になるニュースをピックアップ | 2023年6月版
- 気になるニュースをピックアップ | 2023年5月版
- 気になるニュースをピックアップ | 2023年4月版
- 気になるニュースをピックアップ | 2023年3月版
- 気になるニュースをピックアップ | 2023年2月版
- 気になるニュースをピックアップ | 2023年1月版
- トルコ南部でM7.8の巨大地震発生
- 気になるニュースをピックアップ | 2023年1月24日~1月31日
- 気になるニュースをピックアップ | 2023年1月1日~1月23日
- 副作用が問題視されている新型コロナワクチンに対する様々な意見
- 気になるニュースをピックアップ | 2022年11月21日~12月11日
- 気になるニュースをピックアップ | 2022年11月14日~11月20日
- 気になるニュースをピックアップ | 2022年11月7日~11月13日
- 気になるニュースをピックアップ | 2022年10月31日~11月6日
- 気になるニュースをピックアップ | 2022年10月
- 気になるニュースをピックアップ | 2022年9月
- 気になるニュースをピックアップ | 2022年6月から8月までのまとめ
- アメリカのシンクタンクが新型コロナの後遺症を分析してわかったこと
- 歯止めが利かない、日本人の人口減少。
- 繰り返される自然災害「再び最上川の氾濫」
- 最近気になるニュース:WHOが「サル痘(さるとう)」に緊急事態宣言。
- 選挙演説中、安倍晋三元首相への襲撃事件。海外からの追悼の声。
- 気になるニュースをピックアップ | 2022年1月から5月までのまとめ
- 2月6日更新:今週の看護入試で使える最近の気になるニュース
- 1月29日更新:今週の看護入試で使える最近の気になるニュース
- 1月17日更新:今週の看護入試で使える最近の気になるニュース
- 1月3日更新:今週の看護入試で使える最近の気になるニュース
- 12月27日更新:今週の看護入試で使える最近の気になるニュース
- 看護面接で質問される「SDGS」とは何か?知らなきゃ損!
- 12月20日更新:今週の看護入試で使える最近の気になるニュース
- 気になるニュースをピックアップ | 2021年10月から11月までのまとめ
- 最近気になるニュースで、面接官にインパクトを与えるには3つのことを意識しよう。
- 看護面接の「最近気になるニュース」の正しい答え方
- 旭川で凍死した女子中学生の生前の肉声から判明した真実
- 熱海の土石流から学ぶ人災が起こす自然の脅威
- コロナ感染の妊婦が自宅出産にて新生児が死亡したニュースで感じたこと。
- 全員ワクチン接種完了者7人の命を奪った「ミュー株」は危険。
- 妊娠中の大豆摂取が与える子どもへの影響
- 医療費、75歳以上に2割負担導入がもたらす家計圧迫と思い。
- 大麻草を原料にした医薬品が国内で使用解禁される前に大麻と医療薬品の関係を知っておこう。
- 気になるニュースをピックアップ | 2021年1月から8月までのまとめ
- オンライン服薬指導によって変わる医療社会
- 飲酒が乳がんのリスクを高める理由。
- 新型コロナが骨髄移植の壁となり、臍(さい)帯血移植のニーズが高まっている。
- 「風邪」から学ぶライノウイルスについて
- コロナワクチン接種で引き起こされる「アナフィラキシー」って何?
- 東日本大震災から10年後の余震で見えたSNSの怖さ。
- 「ベビーカーマーク」の浸透。ようやく電車やバスでベビーカーを安心利用できる!?
- 受験生が悩む、「最近気になるニュースの選び方」と「考え方」を徹底解析。
- 薬の成分は何処まで認識すべき!?治療薬に睡眠剤混入で死亡2人・事故件数20件。
- コロナウィルスがもたらした社会への影響。
- 気になるニュースをピックアップ | 2020年1月から10月までのまとめ
- 気になるニュースは「新型コロナウィルス」でOKなのか!?
- コロナの次は三峡ダムが崩壊間近。経済の打撃は中国だけではない!?
- 鹿児島県、熊本県に豪雨をもたらした梅雨前線の恐怖
- 必ず知っておきたい面接で役に立つ「コロナウィルスの知識」受験生必見。
- アフガニスタンで銃撃された中村哲医師が診療より水利事業に力を入れた理由。
- 気になるニュースをピックアップ | 2019年7月から11月までのまとめ
- ベトナムのパラリンピック重量挙げ選手のメダルを競売に出品した理由。
- パラピック金メダリストが選んだ最後のゴールが安楽死だった。
- 歴史的被害を生んだ台風19号とDMAT(災害派遣チーム)の存在。
- シンガポールの世界初の試み!これで糖尿病者と予備軍を救えるのか?
- 今流行の「帯状疱疹」!!年間50万人の高齢者の神経を蝕む前に予防と対策。
- 高齢者の就労対策で一番評価を得ている国と、その方法とは?
- チェコで起きた奇跡!!脳死の女性から女の子の赤ちゃんが誕生
- 100歳以上が7万人超。高齢者とは何をもって言うのか⁉
- 気になるニュースをピックアップ | 2019年1月から6月までのまとめ
- 看護学校が面接で「気になるニュース」を伝える文章の組み立てを知っておこう。
- 看護学校が面接で「気になるニュースを聞く目的」を知っておこう。
- 看護学校の受験で「気になるニュース」を聞かれる理由はこれだった。
- サルに支配される世界が間近まで来ている!?
サルの脳に人間の遺伝子を移植。 - 赤ちゃんの脳性麻痺がお産時に使用した陣痛促進剤だった!?
- 人体の部位は何でも作れちゃう時代が来る!?3Dバイオプリンターが人類を救う。
- 透析って何?透析をしなければ死にいたる理由はこれ!!
- 知ってて当たり前!?ニュースで取り上げられている医療言語は要チェック!!
- 人の寿命はいつまで?近い未来に老化の調整ができるかも!?
- 障害者雇用数の水増し問題は知ってて当たり前!?看護入試で聞かれるかも。
- ゲノム編集による人体の行く末は「幸」か「不幸」か?
- 医師不足を補う「人工知能AI」が医療ミスをすれば誰の責任!?
- 大阪北部地震に続き、歴史的な西日本豪雨災害!!西日本に何が起きている!?
- 日本禁煙学会が「タバコが薬物」であると発表!!依存は「コカイン・ヘロイン」に次ぐ。
- 人の命を救っている看護師がなぜこんな目に!?奪われた命は決して戻らない。
- まだまだ医療ミスがなくならない!?その原点には、人のマイナス部分に潜んでいる。
- 真相はいかに!?看護師としてどうしてこのような過ちを犯したのか!?
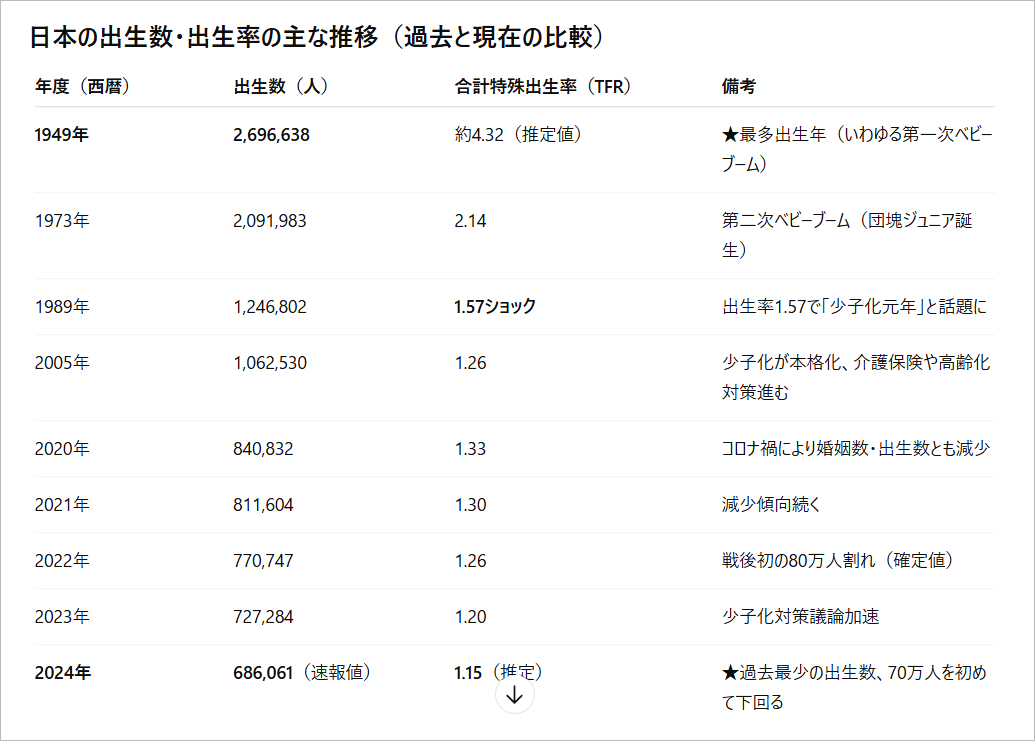
- 今年もまた、出生率の低下・・・今後の日本はいったい誰のもの!?
- 看護受験には必須。ナイチンゲールの存在は絶対に覚えておくべき!!
- インターネットで販売されている薬は本当に大丈夫?購入先には要注意!!
- 夢がある看護国家資格の合格率!!卒業すれば、そのほとんどが看護師になれる。
- 今年もヒアリが出現?夏場にかけてお子様には要注意!!
- 専門実践教育訓練給付金が3年間から4年間に変更になるかも!?社会人には朗報!!
- はしか(麻疹)が猛威をふるいかけ!?国内外で要注意!!
- マライア・キャリーが双極性障害。誰もがあこがれた7オクターブ歌手になぜ?双極性障害とは。
- 看護師として誇りに思う「土俵上」での人命救助に感銘。
- 約5000人の外国人看護師・介護福祉士が誕生・・・高齢化社会の助けとなるか?
- 介護職員の虐待が増加・・・そのストレスとフォローは誰がする?
- これから注目されるオンライン診療!!利用者の不安は!?メリットデメリットはこれ。
- 高齢者の一人暮らしが4人に1人・・・このままで大丈夫!?
- 「事前指示書」について賛否両論!?あなたならどっちを選択しますか?
- 多くの人が知らなかった「不妊手術強制問題」何が正しくて、何が間違いなのか!?
- 世界的にも稀少!!273グラムの赤ちゃんが退院間近に迫る。
- 日本人の長生きが凄い。5年連続増加!男女ともに世界2位。
- 野良猫からマダニ感染。感染女性が死に至る残念なニュース
- やはり無痛分娩にはリスクがあるのか?妊婦死亡相次ぐ
- ここまできたか人工知能(AI)!!大腸がんの見逃しを見抜く。
- コレラが中東・アフリカで猛威を・・・日本は大丈夫か?
- 認知症患者が日々増進。政府も大幅に拡充加速決定!!
- かつての「不治の病」梅毒で赤ちゃん5人死亡!!解決法は?
- 道交法の改正で認知症の疑いは免許取消。
- 信頼していた原薬メーカーに中国製混入。
- まさか!!咳止め薬で呼吸困難。小児には「コデイン」配合要注意。
- 恐怖の強毒ヒアリ、夏の薄着には要注意!!
- 禁忌薬の容認で、妊娠と病気の治療を両立できる可能性。
- レット症候群(発達障害)の改善が将来可能かも?
- 恐るべし、蜂蜜が原因で乳児の命を奪うボツリヌス症を引き起こす
- 看護学校の面接で気になるニュース 一人の肝臓が二人を救う。
- 高齢化社会について看護の医療ニュースのまとめ
- 看護学校の面接で気になるニュース点滴バッグに穴
- 看護学校の面接で気になるニュース脳リンパ腫に関して