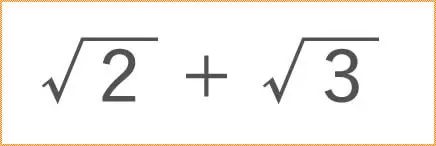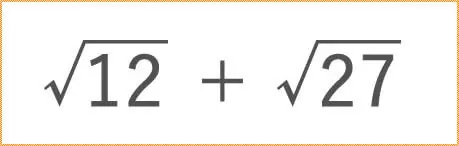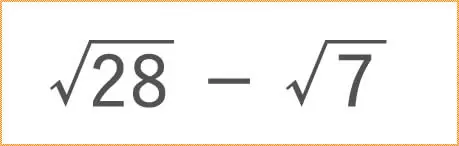日時間分秒

看護学校の受験を合格するには、

高校数学Ⅰと数Aが必ず必要になってきます。

逆に言えば、

これが出来るようになれば、

絶対に、一次試験を突破することが出来ます。

その中でも、「二重根号」は厄介な問題の一つです。

でもコツさえつかめば、実はめちゃくちゃ簡単です。

でも、その前に、

√（ルート）の中の数字をどうすれば、

外に出すことができたのかを

復習しておきましょう。

こういうことでしたよね！？

なので、

二重根号を外す時にも、

この考え方を利用していきます。

それでは、二重根号のお勉強をしていきましょう。

二重根号はどうやって外すの？

では、次の二重根号を簡単にしてください。

どうですか？

できましたか？

これめちゃくちゃ簡単です。

なぜなら、

ですよね？

なので、

この場合の答えは、

このようになりませんか？

ここで、気が付いてほしいのは、

二重根号を外すには、

√（ルート）の中を同数×同数に変えること

なんですよね。

それでは、例題を見てみましょう。

理解できましたか？

ちょっとややこしい部分もありますが、

最後の解き方は、

すごく簡単でしたよね？

しかし、そのやり方だけでは、

なぜ√（ルート）がはずせたのか？

疑問に思ってしまう部分もあります。

いろいろな問題に対応できるように、

是非やり方を覚えておいてくださいね。

• «vol.10：実数 : √（ルート）の整数部分と小数部分の計算
• 「実数」の完全版の初めに戻る。»

フォローして今すぐ看護受験情報をGET

日時間分秒

看護学校の受験問題には、

いくつか出題されるパターンが決まっています。

その中でも、

√（ルート）の「整数部分」と「小数部分」

を聞かれることも多いです。

当看護予備校でも、

毎年学生様にこの部分は確実に

理解してもらっています。

それだけ落としたくない問題でもあります。

それでは、√（ルート）の「整数部分」と「小数部分」をみてみましょう。

√（ルート）の「整数部分」って何？

そもそも、√（ルート）ってなんでしょうか？

きっちりとした数字が出ないものですよね？

下記の√（ルート）の例を見てみましょう。

このように、

計算してもしきれないものを√（ルート）で表します。

そこで、看護入試で問われるものは、

ルートの整数部分は何ですか？

と聞かれます。

では、下のルートの整数部分はいくつですか？

できましたか？

そもそも3√2とは何か？

見てみましょう。

理解できましたか？

このようにして、整数部分を見つけます。

では次に、√（ルート）の「小数部分」を見つけてみましょう。

√（ルート）の「小数部分」はどうするの？

これは、上記の問題を理解できていれば

めちゃくちゃ簡単です。

その理由は、

引き算をするだけでいいんです。

では例題を見てみましょう。

どうでしたか？

簡単に言えば、

√（ルート）から整数を引けば「小数部分」が出てくる

わけですよね。

この形を絶対に忘れないで下さいね。

• «vol.9：実数 : √（ルート）を有理化する意味はこれでわかる。
• vol.11：二重根号の解き方はこれで完璧。»

フォローして今すぐ看護受験情報をGET

日時間分秒

看護学校の受験勉強も進めていくと、

色々な単元の問題が出題されています。

その中でも、

√（ルート）を使う問題は必ず１問

は出題されています。

そして、

簡単な問題が出題されればいいのですが、

ややこしい問題が出題されますよね。

それが、

有理化を使った問題です。

それでは、まず下の問題を解いてみてください。

これは簡単でしたか？

この場合は、

分母が揃っていないので通分

をしましょうね。

では、通分も含めて説明していきます。

できましたか？

それでは、次にこの問題を解いてみてください。

できましたか？

通分するところまでは、

上の問題と同じなのですが、

途中で大切な部分がでてくるので

よく見てくださいね。

では、説明していきます。

有理化は理解できましたか？

分数の分母に√（ルート）を残しておくと間違い

になるので注意してくださいね。

• «vol.8：実数 : √（ルート）には素因数分解が必須
• vol.10：実数 : √（ルート）の整数部分と小数部分の計算»

フォローして今すぐ看護受験情報をGET

日時間分秒

本日も、看護数学のための

「プチ授業」を始めていきます。

前回や前々回の√（ルート）お勉強で、

気になる部分はなかったですか？

例えば

確かに、√18ぐらいの数字の大きさだと

頭の中で考えることも出来るかもしれませんが、

この場合はどうでしょうか？

正直厳しいですよね。

そこで、活躍するのが

素因数分解

というものです。

√（ルート）を整理するには、

とにかく数字を小さくする必要があります。

皆さんは、素数はご存知ですか？

それでは説明していきますね。

素数って何？

素数は理解できましたか？

掛け算のパターンが

１×？

のものだけでしたよね。

では、素数を使って今から素因数分解をしてみます。

素因数分解のやり方はこれで完璧。

どうですか？

理解できましたか？

ついつい割り算だから

大きな数で割ってしまいそうですが、

絶対にNGです。

素因数分解は

２からスタートすべし

です。

なので、これからは√（ルート）を見れば

簡単にすることを心がけてください。

次回は、√（ルート）の王様「有理化」を勉強しましょう。

• «vol.7：実数 : √（ルート）の掛け算と引き算
• vol.9：実数 : √（ルート）を有理化する意味はこれでわかる。»

フォローして今すぐ看護受験情報をGET

日時間分秒

受験生の皆様、勉強ははかどっていますか？

今年度、看護学校の受験に合格された学生様は

本当におめでとうございます。

「まさか合格できるなんて夢みたい！！」

当看護予備校で合格されている学生様は、

みんな口を揃えて言います。

次年度の合格はあなたですね。

すでに、看護学校の受験に向けて

受験生の皆様が続々と勉強し始めています。

乗り遅れないためにも一日でも早く、

看護予備校に通って看護受験を目指さなければ、

近年の看護受験合格は難しくなっています。

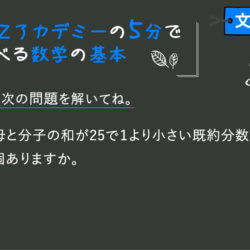
では、本題と戻りましょう。

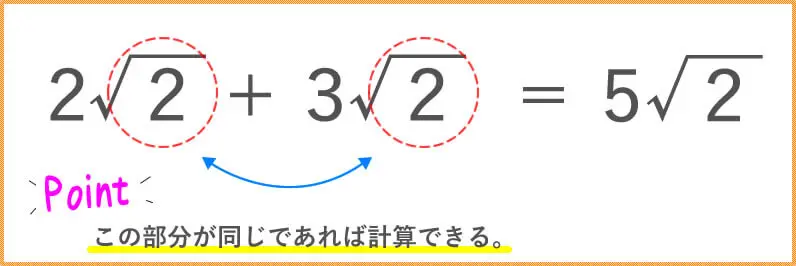
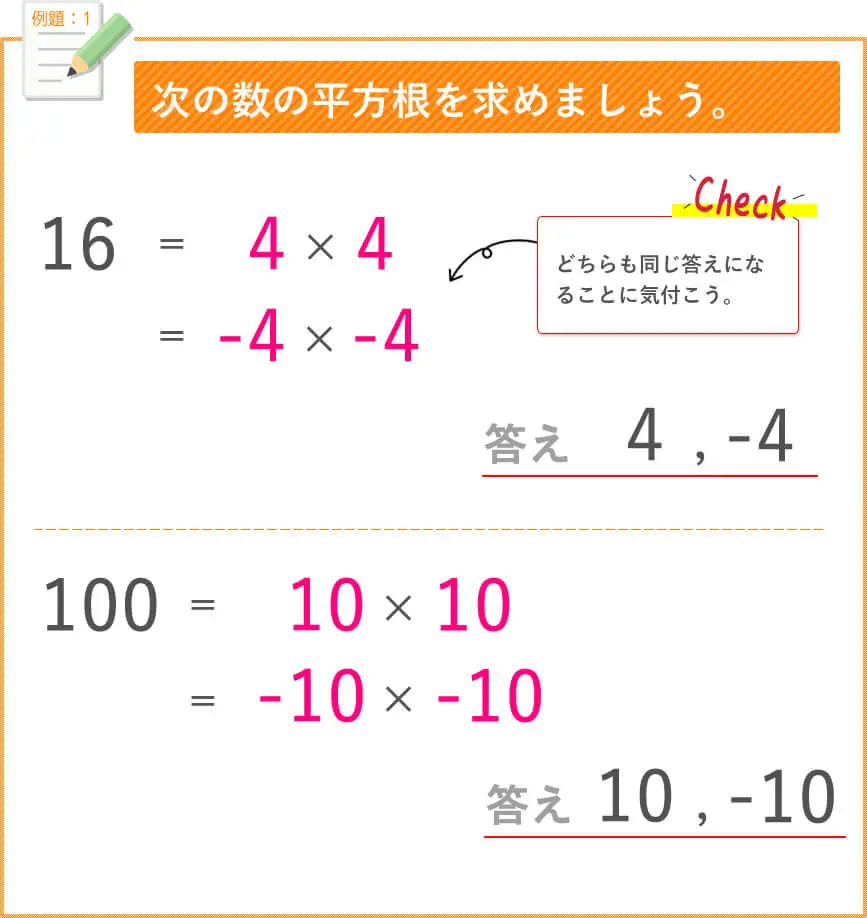
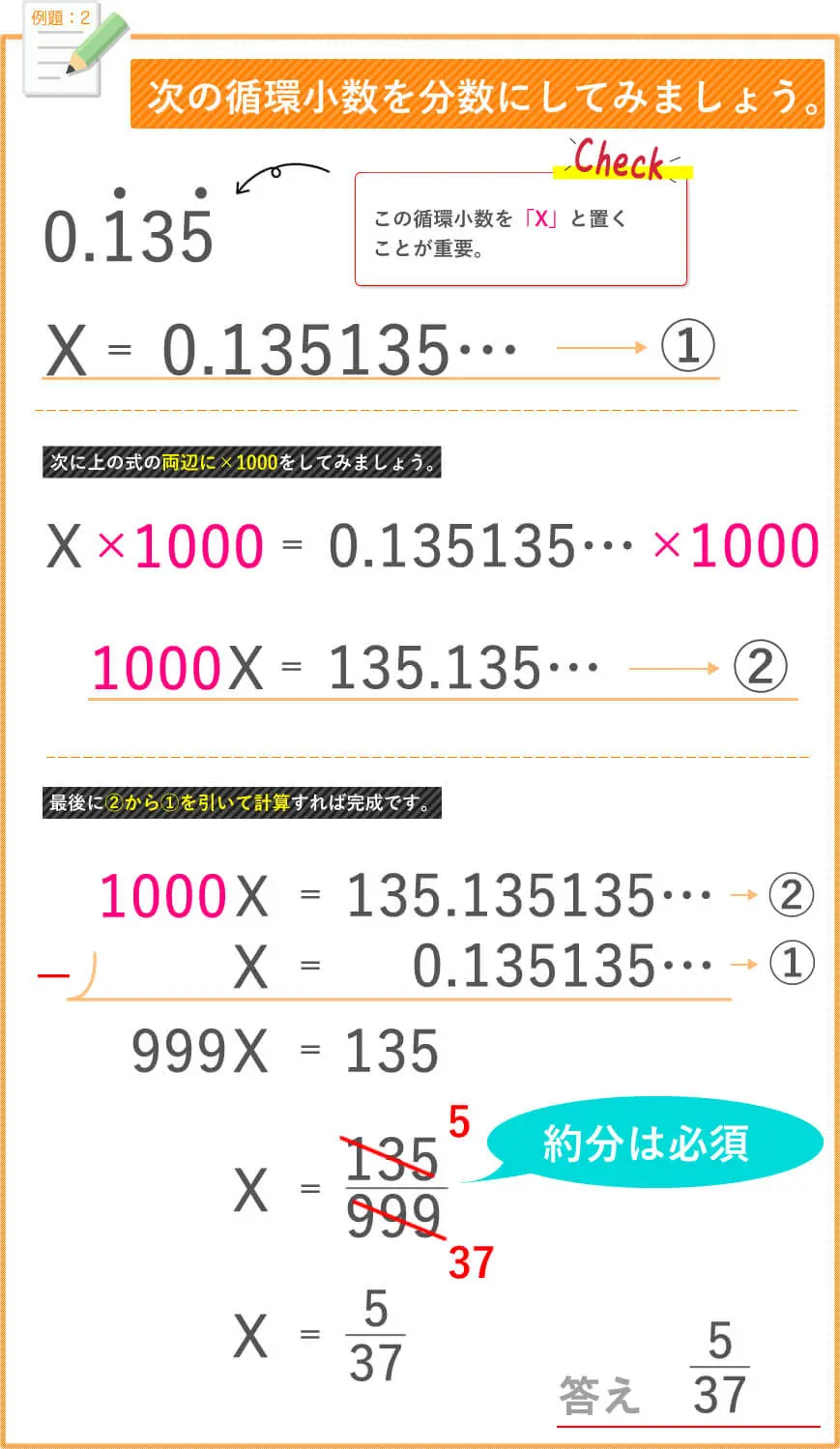
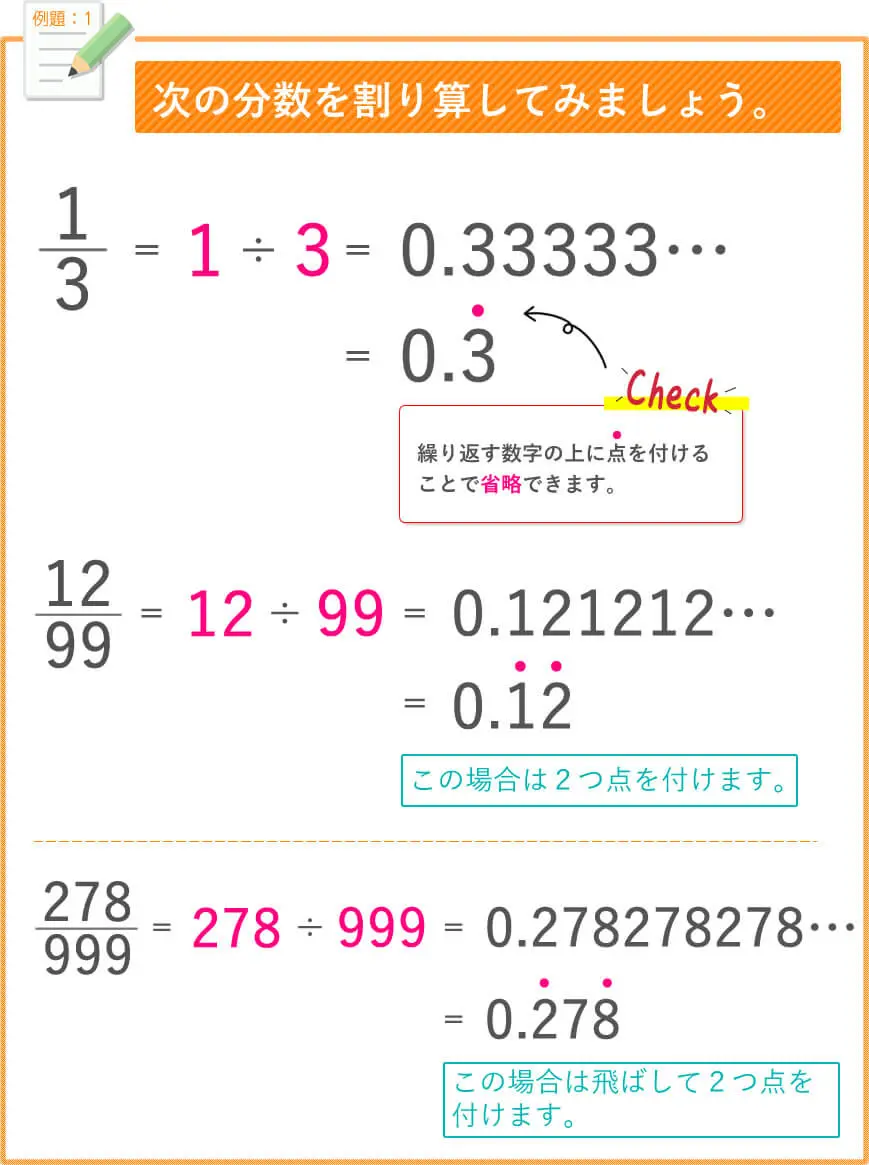
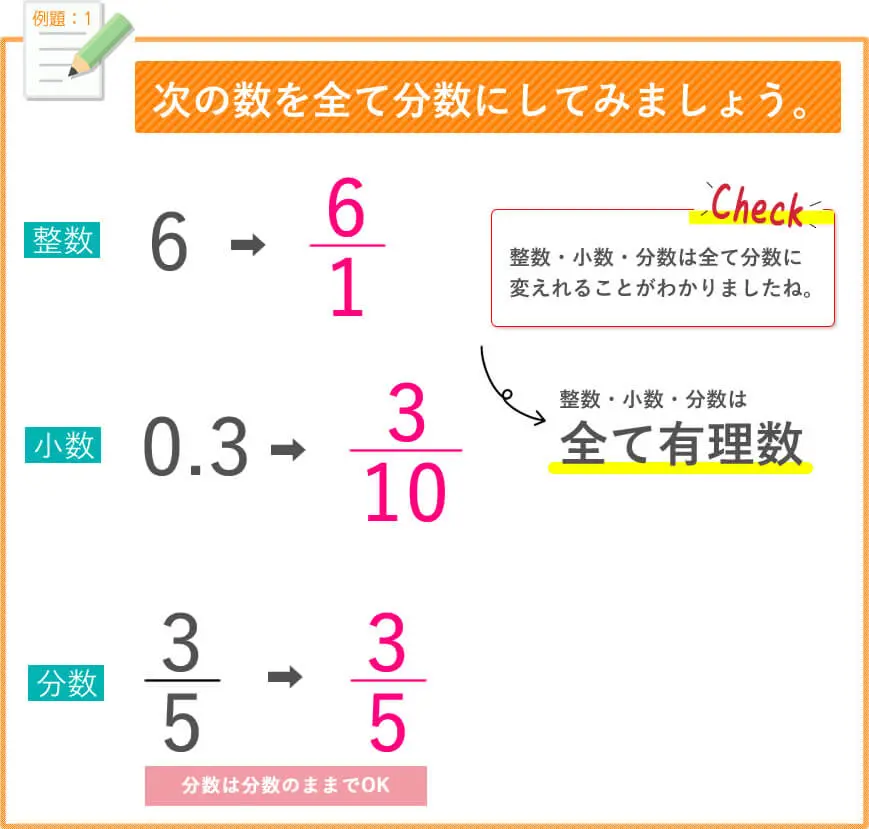
前回は、√（ルート）の足し算と引き算のお勉強をしましたね。

では、今回は、

√（ルート）の掛け算と割り算のプチ授業を行います。

√（ルート）の掛け算ってどうするの？

実は、√（ルート）の掛け算は

そのまま掛け算するだけ

でいいんですよね。

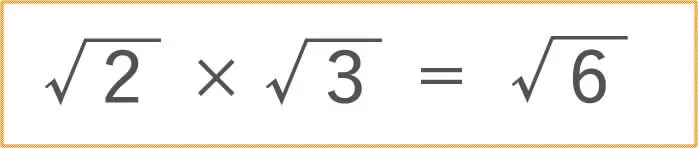
思ったよりも簡単でしたか？

掛け算は意外とシンプルなんですよね。

でもここで一つ問題があります。

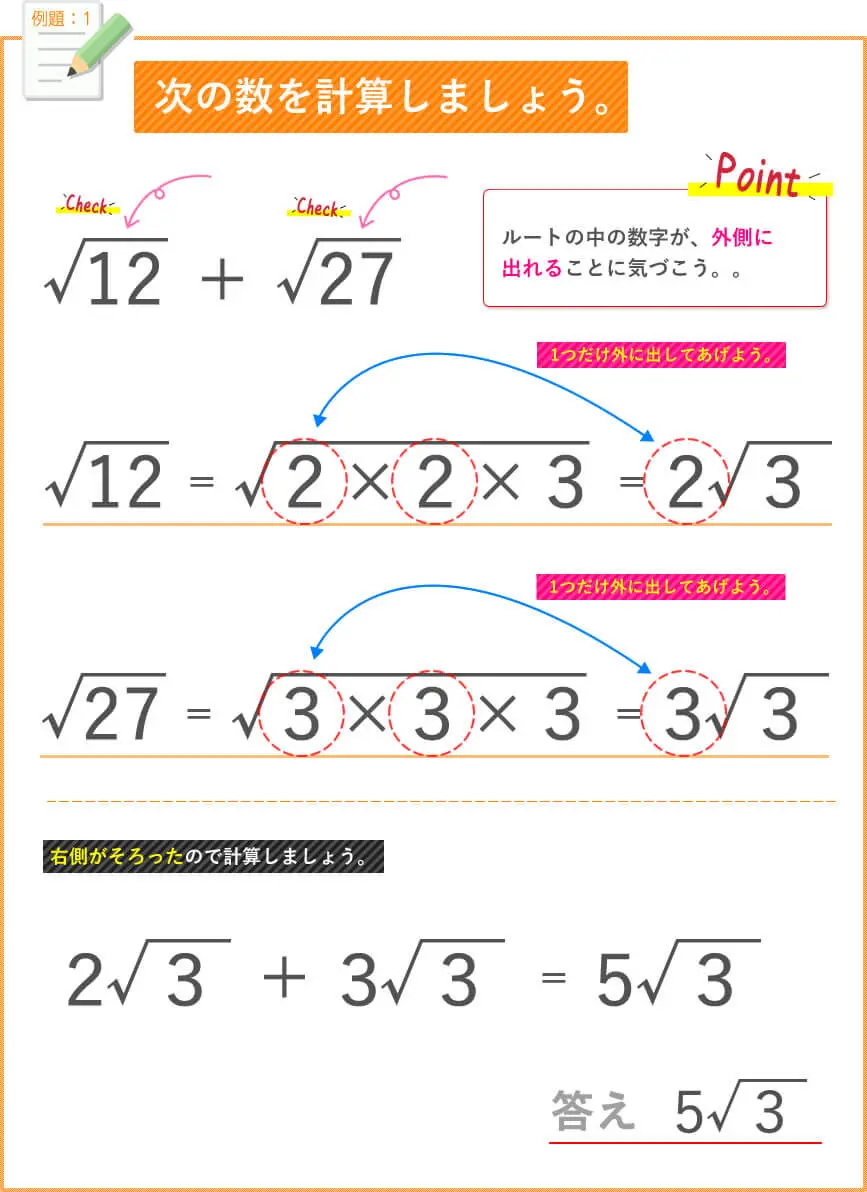
次の場合はどうでしょうか？

これは、絶対にしてはいけません。

何をしたらいけないの？

と思いますよね。

では、解説していきます。

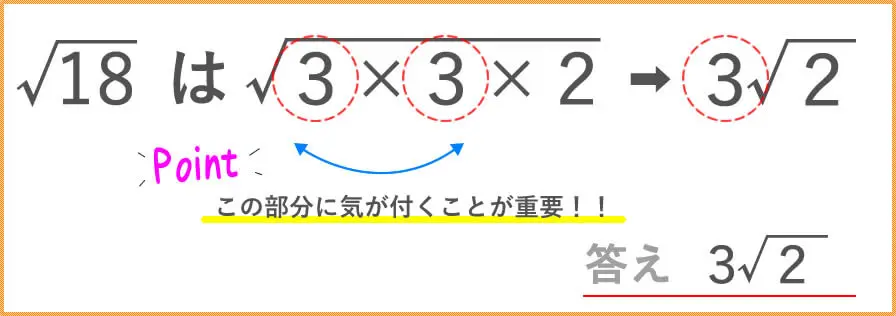
掛け算すると答えはすぐに

求めれるのですが、

最後の最後まで気を付けておかなければいけない

のが√（ルート）の掛け算なんですよね。

では次に√（ルート）の割り算を見てみましょう。

√（ルート）の割り算ってどうするの？

早速例題を見てみましょう。

ここで気を付けておく点は、

・ルートはルート同士
・ルートの外は、外同士

ですね。

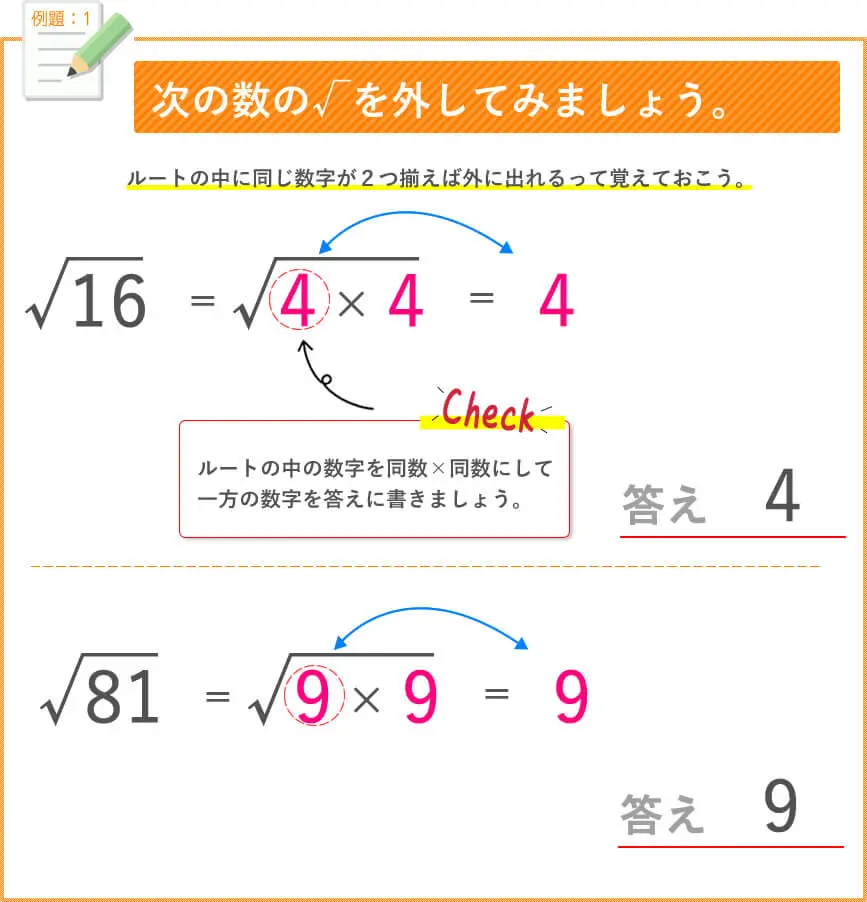
これで√（ルート）の基本はおしまいです。

次回からは看護学校の受験に出てくる

√（ルート）の難易度の高い問題をしてます。

• «vol.6：実数 : √（ルート）の足し算と引き算
• vol.8：実数 : √（ルート）には素因数分解が必須»

フォローして今すぐ看護受験情報をGET

日時間分秒

本日も看護学校合格のご報告有難うございました。

これも皆様が、

当看護予備校の看護受験専門の基礎学習プランを

地道に積み重ねた結果だと思います。

頑張っている人は、

必ず看護学校に合格できますね。

では、今回もこれから看護学校の受験に向けて

受験勉強に挑戦する学生に向けての

プチ授業を始めていきます。

前回は√（ルート）の仕組みを勉強しましたね。

本日は

「√（ルート）の足し算と引き算」

をしていきたいと思います。

√（ルート）の足し算ってどうするの？

では、いきなりですが

これって計算できると思いますか？

もしかして、

√5とかって思いましたか？

残念ながら、不正解です。

これは計算できません。

例えば

ｘ+ｙは計算できますか？

できませんよね。

それと同じく、

√2と√3は全く別物

なんですよね。

では、次にこれは計算できますか？

これは、計算できます。

答えは、5√2

となります。

このように√（ルート）を計算するときは、

必ず右側がそろっている必要

があります。

では、こんな場合はどうでしょうか？

実は、計算できます。

では、計算の仕方を見ていきましょう。

理解できましたか？

最後に、

√（ルート）の引き算

もしておきましょう。

どうですか？

できましたか？

この場合は、

√7は変形できませんよね？

なので、

√28にだけ注目

してみましょう。

このように、足し算でも引き算でも

まず

ルートが整理できるか？できないのか？

これを調べる必要があります。

次回は、√（ルート）の掛け算と割り算をしてみましょう。

• «vol.5：実数 : √（ルート）の外し方とつけ方
• vol.7：実数 : √（ルート）の掛け算と引き算»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回は、「平方根」のお勉強をしましたね。

今回は、前回の内容とかぶる部分もありますが、

これを理解しておくことで、

今後の√（ルート）の問題に対して、

スムーズに理解することができます。

そもそも、

√（ルート）って何であるの？

ということも気になりますよね。

例えば、

正方形25㎠の面積を考えた時

このように

５×５になりますよね！？

では、

正方形23㎠の面積はどうでしょうか。

上記のように分けることはできますか？

無理ですよね。

こんな時には√（ルート）を使うしか方法がないんです。

なので、うまく

同数×同数が出来ないときは

このように√（ルート）を使って

表現をしてあげます。

それでは、例題を見ていきましょう。

このように

√（ルート）の中に入っている数字は、

外に出してあげること

が出来ます。

ではその逆もやってみましょう。

それでは、例題を見てみましょう。

できましたか？

こっちのパターンは少ないのですが、

√（ルート）の仕組みはしっかりと覚えておきましょう。

次回は√（ルート）を使って計算していきます。

• «vol.4：実数 : 平方根とルート
• vol.6：実数 : √（ルート）の足し算と引き算»

フォローして今すぐ看護受験情報をGET

日時間分秒

看護学校の受験問題と言えば

必ず「平方根や√（ルート）」が出題されます。

これは、中学３年生で学ぶ内容ですが、

勉強から遠ざかっている人にとっては

苦手な範囲でもあります。

そこで、今回は「平方根や√（ルート）」の基本を説明します。

平方根って何？

平方根とは、

平方すると元の値に等しくなる数

なのですが、

まず「平方？」ってなるかもしれません。

これは、

同じ数どうしを掛け算することです。

例えば、「９」という数字にしたければ

３×３ですよね？

ただこれでは、小学生の考え方になってしまいます。

中学数学では「-（マイナス）」のお勉強

をしたと思いますが、

-3×-3も9

になりますよね。

なので、

この「９の平方」の答えは、「3,-3」になります。

では例題を見てみましょう。

では、なぜ√（ルート）なんているの？

と思うかもしれないので、

今から説明していきます。

√（ルート）って何？

例えば、

9のように3×3

16のように4×4

25のように5×5

と綺麗な数字で分けることができるのですが、

2はどうですか？

分けることが出来ないですよね？

5はどうですか？

これも分けることが出来ないですよね？

こういう時に

「√（ルート）」が便利

なんですよね。

では例題を見てみましょう。

これで、同数×同数にできなくても

二つに分けることができましたね。

√（ルート）の考え方はこれが基本になるので

是非覚えておいてくださいね。

• «vol.3：実数 : 循環小数の計算
• vol.5：実数 : √（ルート）の外し方とつけ方»

フォローして今すぐ看護受験情報をGET

日時間分秒

看護学校の受験問題には、

循環小数から分数に戻す問題が

出題されます。

学生の皆様は、

分数から循環小数に直すのは

簡単にできるのですが、

循環小数から分数は

どうやら苦手なようです。

では、今回は、循環小数から分数に直してみましょう。

大切なことは、

循環小数を「X」と置くことが大切です。

後は、

小数第一の位なのか？

それとも

小数第二位の位なのか？

またまた

小数第三位の位なのか？

で判断をしていきます。

それでは例題を見てみましょう。

なぜ「×10」を掛けたのかわかりますか？

これは、循環小数を

引き算して消したい

からなんですよね。

なので、

例えば、

0.1212121・・・であれば

0.12/・・・

で区切ることができるので、

「×100」になります。

それではもう一つ例を見ておきましょう。

ケタが大きくなっても

「×□□□」の部分を変化させれば、

解き方は同じでしたよね。

循環小数を分数で表す時は

必ずこの解き方を使ってくださいね。

• «vol.2：実数 : 循環小数って何？
• vol.4：実数 : 平方根とルート»

フォローして今すぐ看護受験情報をGET

日時間分秒

先日は、「有理数」と「無理数」のお話をしましたね。

理解できましたか？

徐々に聞きなれない言葉が出てきますが、

一つずつ理解していきましょう。

それでは、本日は

「循環小数」

この言葉の勉強をしていきましょう。

「循環小数」って何？

この「循環小数」というのは、

分数を割り算した後に、

同じ数字が繰り返すことです。

割り算は小学生で学びましたよね？

覚えていますか？

実は、その中に循環小数がひそんでいたんですよね。

もし割り算の仕方を忘れていたら

この機会に復習してみて下さいね。

それでは、例題を見てみましょう。

どうですか？

いくつか種類がありましたね。

「循環小数」は

繰り返す文字の上に点を打つだけ

なので覚えておいてくださいね。

本日は

分数　→　循環小数

でしたが、

次回は

循環小数　→　分数

のお勉強をしてみましょう。

これは、看護学校の受験問題に含まれていますよ。

• «vol.1：実数 : 有理数と無理数って何？
• vol.3：実数 : 循環小数の計算»

フォローして今すぐ看護受験情報をGET

日時間分秒

高校数学の勉強をしていると

時折、聞きなれない言葉が出てきます。

中学数学であれば、

「整数」「小数」「分数」「ルート」「π（パイ）」

と一つずつの文字を丁寧に説明してくれているのですが、

高校数学の場合は

大きくざっくりとわけて説明している時があります。

その中でも「有理数」と「無理数」

という言葉はよく出てくるので覚えておきましょう。

「有理数」って何？

実はめちゃくちゃ簡単です。

分数で表すことができる数は

すべて有理数です。

では、例を見てみましょう。

この見極めのコツは、

先ほども説明しましたが、

数字を見て分数にできれば、

全て、

有理数

となります。

では続いて「無理数」のお勉強をしましょう。

「無理数」って何？

「無理数」は文字を見ればわかるのですが

無理やり作った数

です。

通常では考えることのできない数字、

例えば

√（ルート）であったりπ（パイ）

これらは、分数に変えることが出来ないので、

無理数

となります。

と、ここで気になるのが

「０の存在」

ですよね。

ちなみに、０（ゼロ）は整数に含まれるので、

分数にできなくても、

有理数になります。

• «「実数」の完全版の初めに戻る。
• vol.2：実数 : 循環小数って何？»

フォローして今すぐ看護受験情報をGET

日時間分秒

今まで、「展開」や「因数分解」の公式を勉強してきましたね。

いよいよ、受験問題です。

看護学校の受験問題には、

必ず計算問題が出題されるのですが、

その中でも、

「たすき掛け」の因数分解は必須です。

それでは、まずたすき掛けの計算の公式を見てみましょう。

たすき掛けの公式

何これ？

全く理解できないんだけど・・・

なんて思いましたか？

確かに、文字だけ見ていると

目がおかしくなりそうですよね。

それでは、これを踏まえたうえで例題を解いてみましょう。

どうですか？

わかりましたか？

この「たすき掛けの計算」のところで大切なのは、

式中の「-11xy」と、赤い点線の部分の答え

が同じになるように

何通りも試す必要があります。

これが結構面倒くさいのですが、

ここさえ乗り越えれば、

実は、それほど難しい問題ではないんですよね。

しかし、慣れるまでは時間がかかると思うので、

早くなれることが出来るように、

何度も解いてみてくださいね。

• «vol.16：数と式 : 因数分解の公式【3乗の公式 その2】
• 「数と式」の完全版の初めに戻る»

フォローして今すぐ看護受験情報をGET

日時間分秒

昨年は、格別の御厚情を賜り、厚く御礼を申し上げます。

当、看護予備校の学生の皆様の頑張りのおかげにて

非常に高い合格実績を達成させて頂きありがとうございました。

本年も社員一同、

「本学の学生様」又「これから看護学校の受験を目指されている皆様」

にご満足いただけるサービスを心がける所存でございますので、

何卒、昨年同様のご愛顧を賜わりますようお願い申し上げます。

また、１月は一般試験が続きます。

受験生の皆様は、1日1日辛い日々が続きますが、

できるだけ楽しんで、

受験勉強に取り組んでいきましょう。

本年もどうぞ宜しくお願い申し上げます。

新年は１月４日（金）から平常授業とさせていただきます。

平成31年 元旦　

【小論文の対策】

【志望動機書・面接の対策】

フォローして今すぐ看護受験情報をGET