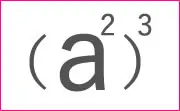前回までは、「中学数学」のおさらいでしたね。
いよいよ、ここからは
「高校数学」に入っていきます。
とは言っても、
数学は
「中学数学」から「高校数学」まで繋がっています。
もし、これから看護学校の入試にチャレンジしようと
思っている学生様は
「中学数学」を完璧にした後に
「高校数学」の勉強をすることをお勧めします。
その方が、自力がつき
さまざまな問題にチャレンジすることができます。
難関である看護学校受験に合格するためには
基礎学習が重要です。
では、本日は、
「高校数学」の「3乗の公式」を
勉強していきましょう。
3乗の公式って何?
中学数学では、「2乗までの公式」しか
学びませんが、高校数学では
「3乗までの公式」ができて当たり前になってきます。
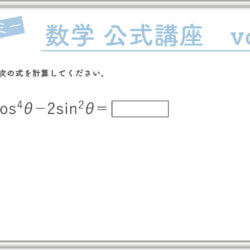
それでは、公式を見てみましょう。

長い・・・
って思いましたか?
確かに慣れるまでは長く感じます。
でも、この問題は
各看護学校の入試で出題されています。
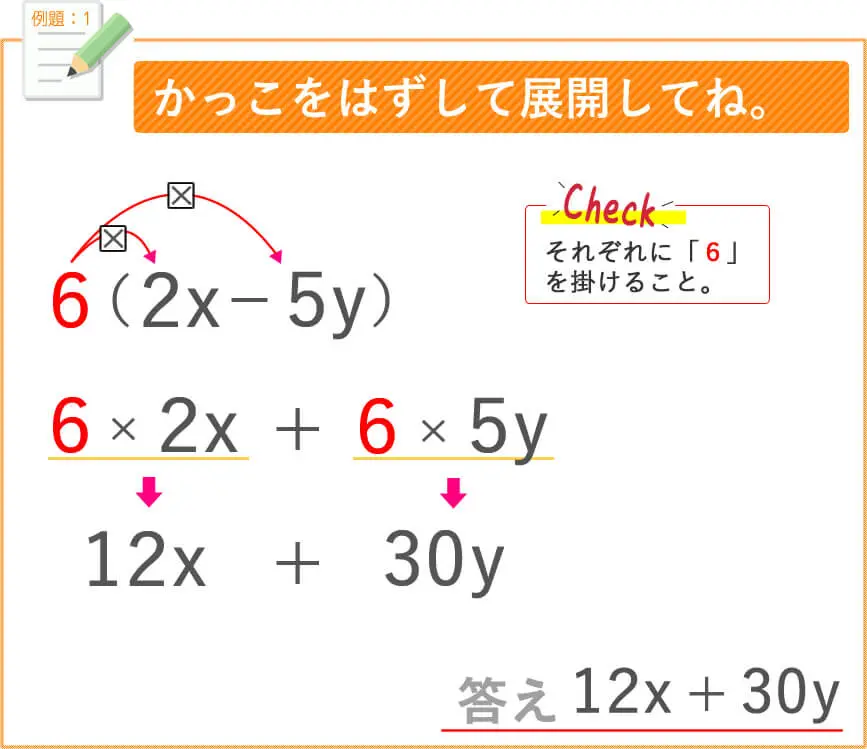
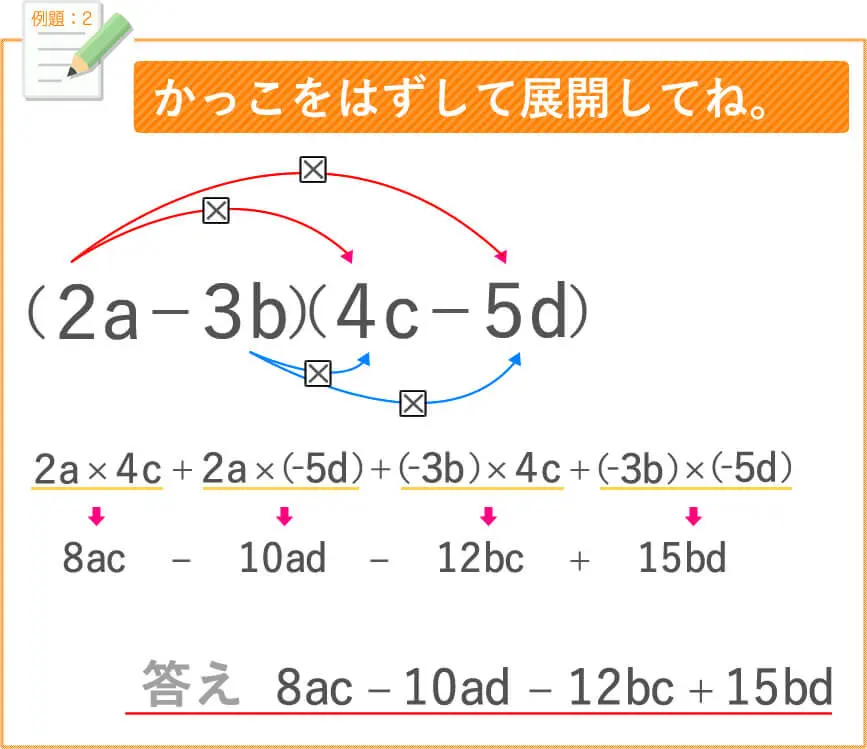
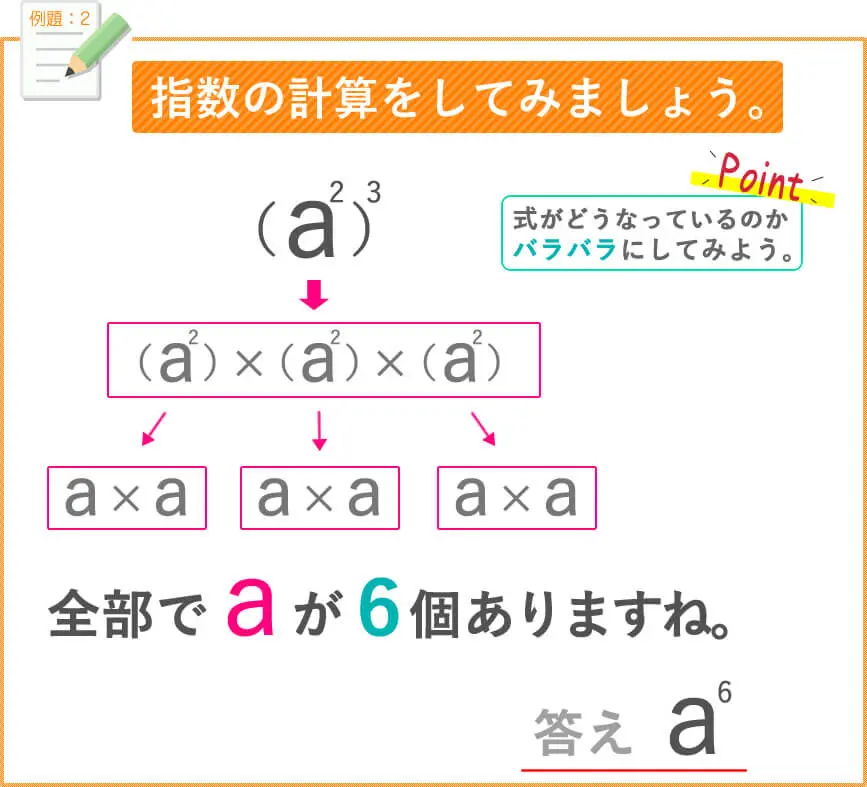
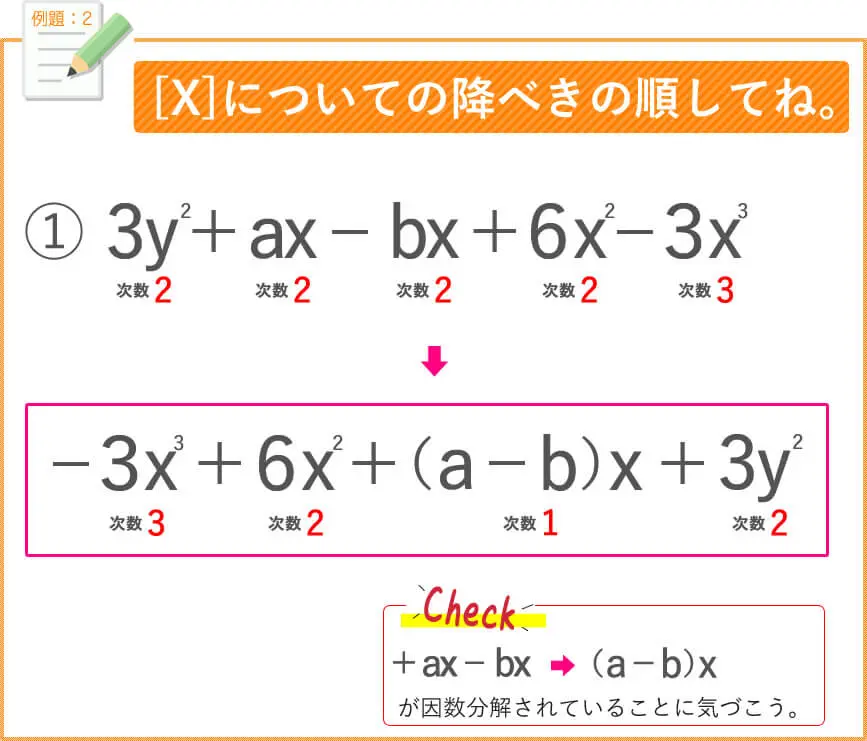
では、例題をしてみましょう。

できましたか?
もちろん、これ一題だけでは
自分のものにはならないので、
受験までにたくさん類似した問題をしましょう。
次回はもう1パターンの「3乗の公式」を勉強しましょう。