命題 : 反例 vol.3：３回読めば、絶対理解できる看護受験数学

命題の反例とは？

命題の問題の答えが「真」でなく「偽」であると時に

「反例」も答えなさい。

と言われます。

要するに、

あなたが「偽」だと答えたのであれば、その理由を言ってよ。

と聞かれているのです。

ここでもう一度、命題の答え方を復習をしておきます。

このように答えましたよね？

この「偽」の時には必ず「反例」がでます。。

上記にも少し触れましたが、

「本当に間違っているなら理由を言ってよ？」

とツッコまれていると思ってください。

そして自分が答えた理由を、相手に理解してもらうために例を書くことを

「命題」では「反例」と言います。

ちなみに、問題によっては

「反例」が何パターンか出る場合もあります。

そんな時には、

では、一つ例題を解いてみましょう。

日本語のまま見るとわかりにくいので

まずは、「⇒」を使って「仮定」と「結論」を書き出してみます。

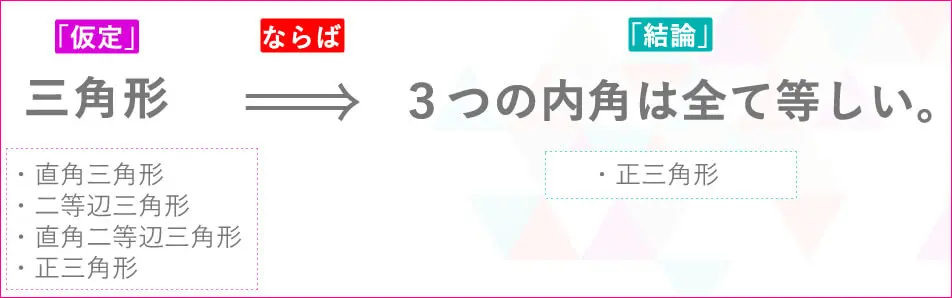
三角形もいくつか種類があります。

そして、命題の考え方ですが、

そして

でしたよね。

それではもう一度、問題を見てみましょう。

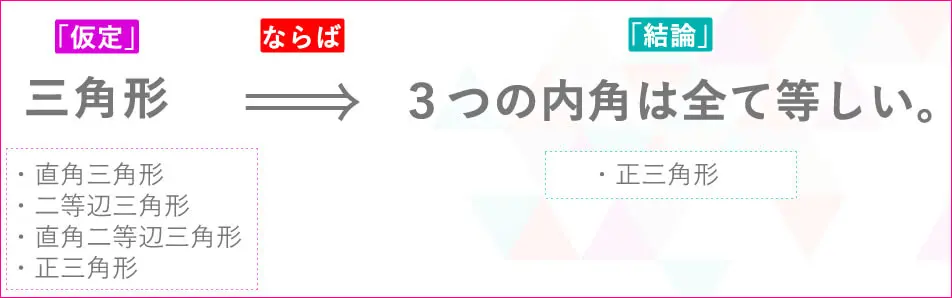
結論の中に

「直角三角形」
「二等辺三角形」
「直角二等辺三角形」
「正三角形」

全て含まれていましたか？

含まれていませんね。

含まれているのは、「正三角形」だけです。

なので

答えは、「偽」になります。

ここで

の出番です。

皆さんが書き出した、

・直角三角形
・二等辺三角形
・直角二等辺三角形

のどれでもいいので、

最低１つは書き出しましょうて。

答えの書き方は、

こうすることで、あなたが「偽」と言ったことが証明されます。

それでは、次回の「命題 vol.4」では、これも受験生を悩ます、

十分条件について説明していきます。

• «②命題 : 仮定と結論 vol.2
• ④命題 : 十分条件 vol.4»