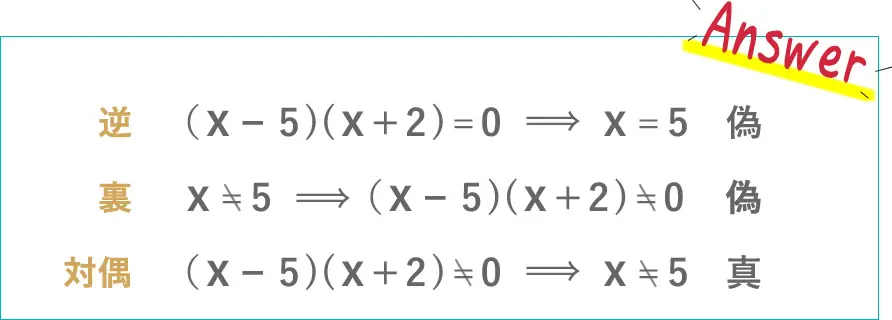命題 : 逆・裏・対偶 vol.8：３回読めば、絶対理解できる看護受験数学

命題の中で一番混乱するのが、

この「逆・裏・対偶」

かもしれませんがじっくり読んでくださいね。

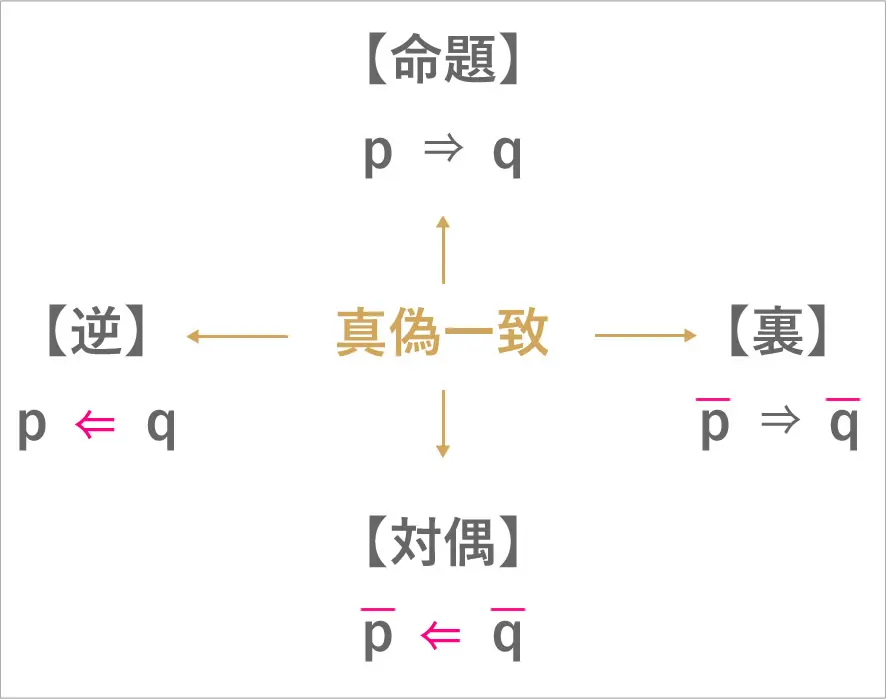
これは「逆・裏・対偶」をわかりやすく図で

表したものです。なぜ、これを

わざわざ覚える必要があるのか？

問題によっては、「AならばB」を

証明することが難しい時に

向かい側の対偶

「BでなければAでない」

を証明すれば素早く答えを導けることがあります。

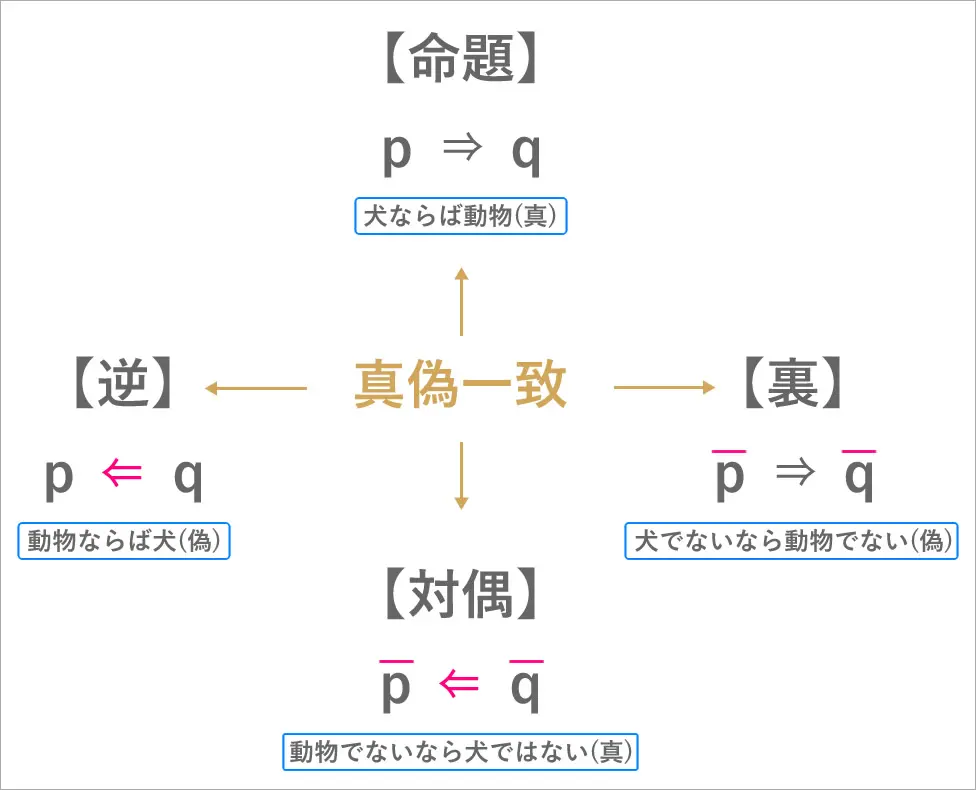
例えば、

「犬は動物である。」と命題がある時、

これは「真」ですが、

「「動物でないなら犬ではない」

これもまた、「真」です。

このように、

「命題」と「対偶」の「真偽」は常に一緒になっています。

そして、「逆と裏」の真・偽も同じになっています。

どうですか？

なんとなくイメージが湧きましたか？

「ならば・なければ」だけを

考えていると、頭が混乱するので、動物などに例えて

自分自身でこの図を書いてください。

では、一つ例題を解いてみましょう。

このような問題が出てきた時は、

とにかく、

書き出すことが重要

です。

このように、一つずつ

「真・偽」について

考えてあげる必要があります。

• «⑦命題 : 否定 vol.7
• 「高校数学の「命題」を８つでポイントで解決」」の最初に戻る»