命題 : 必要条件 vol.5：３回読めば、絶対理解できる看護受験数学

今回は「必要条件」について考えていきますが、

前回学んだ「十分条件」を確実に理解できている必要が

あるので、復習をしておきます。

必要条件を学ぶ前に十分条件の復習

これを確実、頭の中にインプットして下さい。

命題で出題される必要条件とは何か。

「十分条件」はp ⇒ qが「真」

「必要条件」はq ⇒ pが「真」

「十分条件」と「必要条件」を比べると方向が異なるがわかります。

必要条件を例題で確認。

頭の中で整理するのは難しいので「書き出すこと。」が重要です。

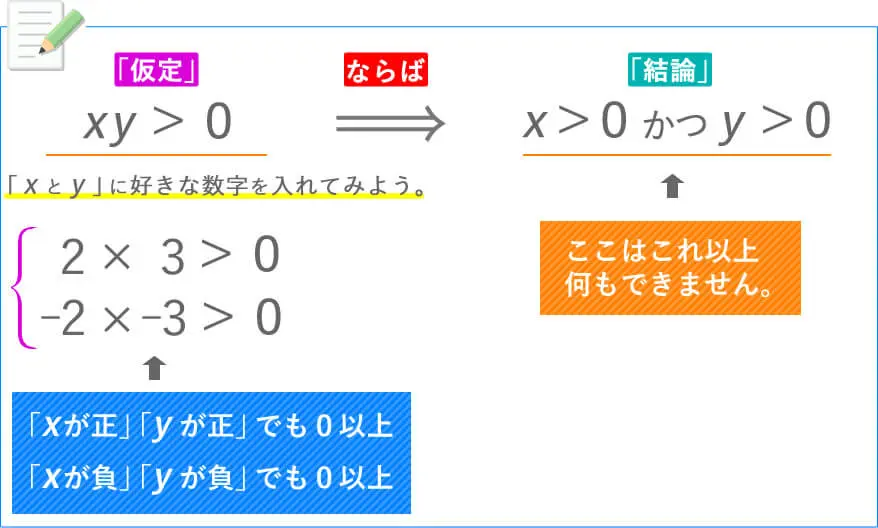
よって

ですよね？

でも、

結論の「ｘ＞０かつ y＞０」

と

仮定の「xが正＞０、ｙが正＞０」

は一致していますよね!?

ここで、「必要条件」

を思い出してみましょう。

の時、

でしたよね？

なので、今回の問題は

今回の問題では、

「pならばｑは（偽）」

かつ

「qならばpは（真）」

と、一方通行になっているので、

「pはqの必要条件である」と言えます。

「十分条件」と見比べて下さい。

• «④命題 : 十分条件 vol.4
• ⑥命題 : 必要十分条件 vol.6»