2次関数 : 共有点の求め方
「高校数学：2次関数の問題に共有点は必須の巻」vol.22

皆さんゴールデンウイークはいかがでしたか！？

いよいよ、夏本番に近づいてきますね。

勉強の進度はいかがですか！？

そろそろ中学３年生の内容をしている学生様は

５月末までには終わらせたいところですね。

とはいっても焦りは厳禁なので、

しっかりと計画を立てて勉強することが大切です。

どんな小さなことでも日課にしてあげることで、

必ず大きな力となります。

それでは、今回も2次関数の勉強をしていきます。

2次関数の共有点って何！？

2次関数の問題では、必ずと言っていいほど共有点の問題が出題されます。

いきなり共有点と言われてもわかりませんよね。

共有点とは、x軸と重なっているところ

をいいます。

それでは、下の放物線を見て下さい。

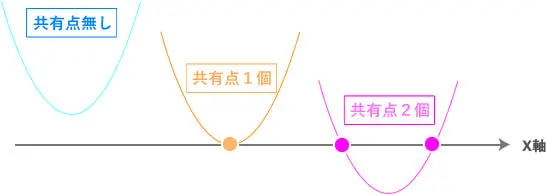
実は、式を見ただけではどのような種類の放物線になるのかわかりません。

青色の放物線 = 共有点無し
オレンジ色 = 共有点1個
紫色 = 共有点２個

なので、まず皆様の頭の中には

この３種類の放物線をイメージするようにしましょう。

それでは例題を解いてみましょう。

まずこの問題を見た時に気が付いてほしいのは、

因数分解ができることです。因数分解の復習はコチラからして下さいね。

ではこの式を因数分解してみましょう。

同じようになりましたか！？

ここで少し、問題を読み返してみると

X軸との共有点の座標

と書いていますよね。

X軸との共有点の座標とはどこのことかわかりますか？

ｙの座標が０

であることを言っているんですよね。

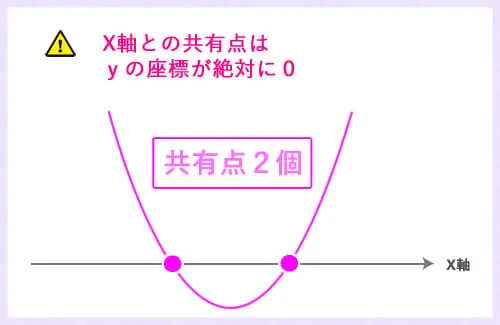
なので、後は先ほど

因数分解した式のyに0を代入してあげます。

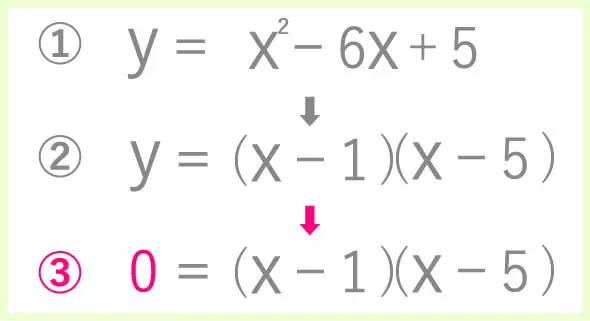
これで後はXを解けば答えになります。

今回の共有点の範囲を答えるには、中学生の知識をたくさん使いましたね。

中学生の範囲がいかに大切なのかがわかります。

看護学校の受験を控えている皆さんにとっては、

焦りと結果を求めてしまいがちですが、

復習には手を抜かず進めることを意識しましょう。

• «Q21.軸に文字を含む場合の最大値と最小値③
• Q23.判別式を使いこなそう。»