日時間分秒

皆さん、看護学校の受験に向けて

準備は進んでいますか？

当看護予備校でも、

次年度に向けて、学生様は着々と

基本勉強を進め力をつけています。

これが受験シーズン到来した時には

必ず大きな力となってくれます。

理解力も一日では身につかないので、

とにかくコツコツ進めていきましょうね。

では、本題に戻り、

今回は「補集合」について勉強していきます。

補集合って何？

集合では普段聞きなれない

日本語がたくさん出てきましたね。

その１：部分集合（忘れた人は ➡click）
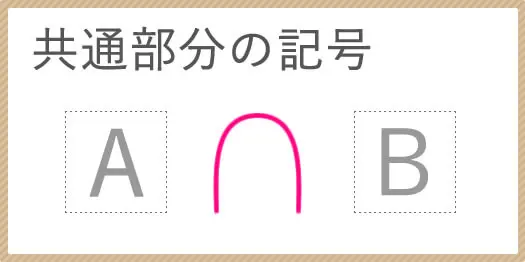
その２：共通部分（忘れた人は ➡click）
その３：和集合（忘れた人は ➡click）

この３つの言葉を覚えましたよね。

そして、

今回の「補集合」で大体、

集合の範囲は終了します。

この「補集合」は

今までと

全く逆の部分です。

図で見るとわかりやすいので、

図を書いてみます。

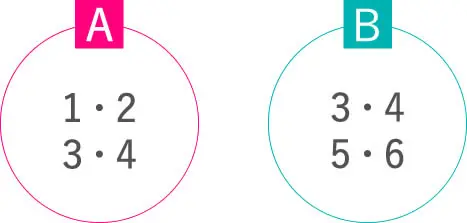
例えば、上のように

緑の四角の中に「A」

があるとします。

では、

そうです。

「A」以外ですよね。

単純でしたね。

この部分のことを「補集合」といいます。

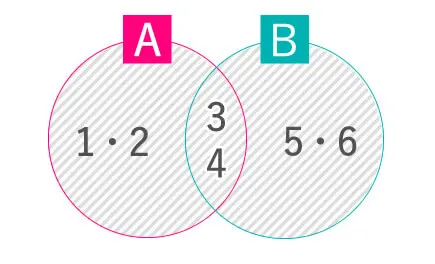
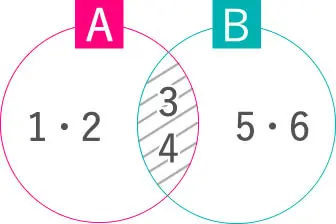
ちなみに、「共通部分」や「和集合」のように

これにも表し方があります。

このように

これで「A」の補集合

と表すことができます。

では、例題を解いてみましょう。

日本語で書くと長ったらしくて

嫌になりますよね。

でも、思い出してみてください。

そうです。

A以外の部分ですよね。

なので、

こんな感じになりますよね。

なので、今回の答えは、

Ā = { 2,4,6 }

となります。

• «不等式と集合が混ざった問題。「見た目が難しい問題の巻」vol.7
• ド・モルガンの法則「頭の混乱には要注意の巻」vol.9»

フォローして今すぐ看護受験情報をGET

日時間分秒

皆様以前に不等式の勉強をしたことを

覚えていますか？

忘れた方は下の「高校数学「方程式と不等式」の完全版」を

見て下さいね。

これは
入試によく出題される問題

でしたよね。

数学問題は、1つの問題の中に、

色々な分野で勉強してきた解き方が

混ざってくるんですよね。

これが、受験生を悩ませる１つでもあります。

では、今回は

「不等式と集合が混ざった問題」を

解いていきます。

さっそく問題を見てみましょう。

何これ・・・

解けない・・・

なんて思いませんでしたか？

では

1つずつ見ていきましょう。

まず

この記号⋂

は共通部分を聞いてましたよね。

なので、

と

の共通部分について考えるのですが、

前回のように

を使えるといいのですが、

きっちりとした数字が答えに出ない

ので、こういう場合には

数直線

を使います。

では、数直線を書いてみます。

このように数直線を書くことで、

共通部分がどこなのか？

わかりやすいですよね。

でも、

答えを書くのはまだ早いです。

最後は、しっかりと

この形までかかないと、

答えにならないので気を付けてください。

• «和集合って何？「和集合の記号はカップと呼ぶの巻」vol.6
• 補集合って何？「補集合が受験生を悩ますの巻」vol.8»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回は、「共通部分」について学びましたよね。

覚えると簡単ですが、

知らないとめちゃくちゃ難しく感じます。

これが、集合の問題のやらしいところです。

そして、

本日は「和集合」

について学びます。

和集合って何？

またしても、

変な日本語が出てきましたが、

でも、

「和」といっているので

足せばいいだけです。

そして、

どんな記号を使えばいいのか？

でしたよね。

今回は、それをひっくり返した

こんな記号を使います。

これは、☕に似ているので

和集合の記号はカップ

と呼ばれたりもします。

では、いったい和集合は

どの部分なのでしょうか？

例えば、問題で

と聞かれると

全部に斜線を塗りましたが、

この通り

全部の要素を答える

だけでいいんです。

それでは、

一つ例題を解いてみましょう。

上記にも書きましたが、

全部答えるだけでいいので、

この当てはまっている数字を

全て答えてあげてください。

なので、今回の答えは、

A∪B = {1,2,3,4,5,6}

になります。

• «共通部分って何？「共通部分の記号はキャップと呼ぶの巻」vol.5
• 不等式と集合が混ざった問題。「見た目が難しい問題の巻」vol.7»

フォローして今すぐ看護受験情報をGET

日時間分秒

すでに看護学校の受験に向けて

スタートをきっていますか？

当看護予備校の学生は、

着々と

「公募入試」「社会人入試」に向けて

受験勉強を始めています。

当看護予備校の学生は、

毎年、

数学で必ず高得点を取ります。

数学を会得するには、

時間と労力がいりますが、

当看護予備校の基礎からの学習が

好評なのは、

確実に実力が上がる

からです。

そして、数学は

あなたの看護受験を絶対に裏切りません。

それでは、

今回も高校看護数学の「集合」について、

プチ授業をやっていきます。

共通部分って何？

またまた、新しい言葉が出てきましたね。

共通部分なんですが、

共通部分を表す記号は

こんな感じで、英語のUの逆を

書いてあげます。

呼び方は、帽子に似ているから

🎩（キャップ）

なんて呼ばれていたりします。

で、どんな感じで使われているかというと、

なんて、

問題では質問されます。

それでは、

例題を解いてみましょう。

要するに、

AとBでかぶっている部分はどこ？

って聞かれているのと

同じなので、

答えは

A⋂B＝{3,4}

となります。

でも、これだけだとちょっと・・・

という方には、

ちょっと図を書いてみます。

この二つの円をくっつけてみます。

このように、

真ん中部分でかぶるところ{3,4}

がありますよね。

これが

今回の問題の答えとなります。

• «部分集合を表す記号。「部分集合の記号は必須の巻」vol.4
• 和集合って何？「和集合の記号はカップと呼ぶの巻」vol.6»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回や前々回で、

「集合」や「部分集合」

のことを勉強してきましたよね。

しかし、日本語で書いていると

長ったらしくて

問題としては不都合

なんですよね。

そこで問題には、

「部分集合の記号」が

使われます。

部分集合の記号の使い方。

では、部分集合の記号って

どんな記号なんでしょうか？

U字磁石のような記号を使います。

そして、点線の四角のところに

比べたいものを書く

だけでいいんです。

例えば、

こんな日本語があれば、

このように書いてあげます。

って言っても

言葉だけだと少しややこしいですよね!?

一つ例を書いてみます。

例えば、

とある動物園があったとします。

この動物園の中には、

クマ・ライオン・ゾウ・キリン・サル・パンダ

がいます。

問題で、

と聞かれれば、

部分集合の記号を使って、

このようにあらわすことが出来ます。

要するに、

・口が開いている方には大きな集合
・口がない方には小さな集合

ですね。

それでは、

例題を解いてみましょう。

そこまで難しくないですよ！？

よく見てみれば、

Bの中にAの数字がすべて含まれています。

なので、答えは

A ⊂ B

となりますよね。

「部分集合の記号」と「不等号の記号」は

似ているので、

どちらが大きい方なのか

わからなくなった時には

思い出して下さいね。

• «部分集合って何？「集合の言葉の意味は超重要の巻」vol.3
• 共通部分って何？「共通部分の記号はキャップと呼ぶの巻」vol.5»

フォローして今すぐ看護受験情報をGET

日時間分秒

看護学校の受験に向けて

高校数学を解いていると、

毎回色々な言葉が出てきますよね。

時には嫌になる時もあるかもしれませんが、

こればっかりは、

1つずつ覚えるしかないので、

頑張っていきましょう。

それでは、今回は

部分集合についてです。

部分集合って何？

言葉だけで見ると難しく

感じるのですが、

部分集合は

家族構成で考えると簡単

なんですよね。

では、１つの家族を書いてみます。

お父さん・お母さん・男の子の子供・女の子の子供・ペットの犬

この５人とペットが家族構成ですよね。

そして、この集まりは

どんな集合になりますか？

そうです。

田中家の集合

ですよね。

では、この家族を

色々な部分集合に

分けてみます。

なんとなく雰囲気はつかめますよね。

では、次に進みます。

この部分集合で

どういうこと？

と理解できなくなる部分は

次のパターンです。

これら、

一人一人であっても部分集合

と言うんですよね。

さらに、

部分集合には、

何も集まらなかった

という場合もあります。

これも必要なんですよね。

これを∅（空集合）

と呼ぶので

是非、覚えていて下さいね。

まとめてみると

「全体が部分集合」だったり

「集合がない場合も部分集合」だなんて

変な日本語ですよね。

しかし、問題では

必ず答える必要があるので、

抜けてしまうと

不正解になります。

では、

次の問題を解いてみましょう。

数字になると少しイメージが

変わるかもしれませんが、

簡単にいうと、

全てのパターンを書き出してね。

と言われているようなものなので、

書き出してみましょう。

これで、全て出揃いましたよね。

このように、

1つずつ順番に書き出して

答えを書いてあげてください。

• «集合の問題文の意味。「集合の問題文を読み取ろうの巻」vol.2
• 部分集合を表す記号。「部分集合の記号は必須の巻」vol.4»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回は、

集合がどんなものか！？

を勉強しましたね。

例えば前回のように

キャンディー・チョコ・クッキー・ポテトチップス

ぐらいであれば、

問題に書き表すことも

できますが、

集合の中の要素が多くなれば、

いつもいつも全てを

問題文に書き出すことができません。

例えば、

集合A{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}

とあったとします。

これがもし

問題文で書いてあると

多いなぁ・・・

なんて思いませんか？

さらに、

「1000」とか「10000」まで増えると

それこそ、

これだけで、数学の入試問題が

数ページにもなってしまいます。

そこで、これを簡単に

表現している方法があります。

それは、

このように書くことで、

集合A{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}

みたいに

長々と書く必要は

ありませんよね。

では、

1つ問題を読み取ってみましょう。

どうですか？

できましたか？

では、

この問題の解説をしていきます。

問題文には

このような書き方を

しているので、

何を聞かれているのか

読み取ってくださいね。

• «集合と要素って何？「集合の問題は計算不要のラッキー問題の巻」vol.1
• 部分集合って何？「集合の言葉の意味は超重要の巻」vol.3»

フォローして今すぐ看護受験情報をGET

日時間分秒

以前であれば、

看護学校の入試数学に、

「集合や命題」の問題は

チョロっと出題されるぐらいでしたが、

受験生のレベルも上がり、

看護入試問題のレベルが上がっていることで、

各看護学校で、

「集合や命題」の問題が

がっつり入試に出題される傾向に

なっています。

「集合や命題」が嫌いな学生が

たくさんいるのですが、

実は、図に書いて表せば

すごく簡単なんですよね。

例えば、下の画像

キャンディー・チョコ・クッキー・ポテトチップス

これらは何の集まりですか？

そうです。

キャンディー・チョコ・クッキー・ポテトチップスを

一括りにすると

お菓子ですよね。

では、これを数学的に考えてみると、

お菓子（全体）を

集合A

それに含まれている

キャンディー・チョコ・クッキー・ポテトチップスの１つ１つを

要素

と表現されます。

ちなみに、

・要素である時の記号
・要素でないときの記号

まで、あるんですよね。

是非覚えておいてくださいね。

では、どのように

この記号を使うのか！？

1つ問題を解いてみましょう。

記号を使えばいいので、

簡単なのですが、

問題は向きですよね。

これは日本語の順で書いていけばいいので、

となります。

次回は、

「集合の表し方について」

学んでいきましょう。

• «集合のTOPページ
• 集合の問題文の意味。「集合の問題文を読み取ろうの巻」vol.2»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回、前々回と、

「判別式の使い方」

の勉強をしてきましたね。

皆さんは、

下記の内容を覚えていますか？

判別式で調べることができるのは？

・異なる２つの実数解
・重解
・実数解をもたない

でしたよね。

このどれかを、因数分解を使わなくても

すぐにわかることが

判別式の魅力でした。

そして、

今回は判別式の使い方のラスト

実数解をもたない

時の考え方です。

といっても、

全部同じなんですよね。

要は、

これのどれに

「当てはまっているのか。」だけです。

では、

次の問を解いてみましょう。

前回やった問題と似てますよね。

そうなんです。

ほぼ同じなんですよね。

変わるところは、

この最後の

「>０」「=０」「<０」

この部分だけなんですよね。

では、

解説をしていきます。

できましたか？

ほとんど同じでしたよね。

なので、

文章を読んだときに嫌にならずに、

最後までじっくりと見てくださいね。

これと類似した問題が、

看護入試で出題された時には、

思い出してくださいね。

• vol.14：方程式と不等式 : 重解の解き方は判別式ですぐ解ける。
• 「方程式と不等式」の完全版の初めに戻る。»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回は、判別式をどうやって使うのか？

それを勉強しましたよね。

もし、使い方を忘れた方は

前回のvol.13に戻ってみましょう。

で、今回はちょっとした

「判別式を使った文章題」

を解いてみましょう。

その文章中に使われる言葉が、

重解

です。

重解とは何だったのか？

思い出してみましょう。

解（答え）が１つ

しかないということでしたよね。

さらに、

判別式に代入した時には、

でしたよね。

それを踏まえて、

今回の問題を解いてみましょう。

いきなりこんな感じで、

文章題が出題されると

「無理っ・・・」

って拒否反応が出るかもしれませんが、

この問題はすごく簡単なので、

解説を見てくださいね。

文章題を読んだときに

定数ｍって聞かれると

「どうしたらいいの？」

なんて不安になりますが、

前回に解いた

判別式を使う問題

と同じ何ですよね。

意外と簡単なので皆さんにとって

ラッキー問題になるかもしれません。

• vol.13：方程式と不等式 : 判別式で解く問題はこれ！
• vol.15：方程式と不等式 : 実数解をもたないも判別式ですぐ解ける。»

フォローして今すぐ看護受験情報をGET

日時間分秒

前回は、判別式とは何なのか？

それを勉強しましたよね。

この判別式は、

看護学校の受験数学では絶対に使います。

判別式を使う理由は３つでしたよね？

・異なる２つの実数解
・重解
・実数解をもたない

判別式にいれることで、

最終的に

解（答え）が何個出てくるのか？

がわかりました。

では、今回は

判別式を使った問題を

解いてみましょう。

いつもと一緒じゃないの？
因数分解をして解くんでしょ？

なんて思いましたか？

確かに、

因数分解をしてから解くのも

１つの方法ですが、

今回の場合は、

Xの答えを聞いているのではなく

Xの答えが何個出てくるのか

を聞かれています。

だからこそ、

前回の判別式の公式を思い出してください。

これがめちゃくちゃ役に立ちます。

では、

今回の問題の解説を

していきます。

こうすることで、

解の個数を簡単に、

確認することができます。

この問題は、看護受験に本当に大切なので、

絶対に暗記してくださいね。

次回は、判別式を使った文章題を解いてみましょう。

• vol.12：方程式と不等式 : 判別式って何？
• vol.14：方程式と不等式 : 重解の解き方は判別式ですぐ解ける。»

フォローして今すぐ看護受験情報をGET

日時間分秒

本日のプチ授業は、「判別式」についてです。

またまた、変な日本語が出てきましたね。

でもこの判別式はかなり重要

なので、是非覚えてくださいね。

皆さんが、看護学校の受験勉強をしている中で、

学生時代には感じなかった違和感を

数学に感じることがあります。

これって実際に何に使うの？

何のために必要なの？

勉強に、励めば励むほどその存在が気になります。

ですが、数学は皆様の生活の原点（０）でもあるんですよね。

現在勉強している「二次方程式」も

そもそも何のか？

何に使うのか？

これは、今後学ぶ

「二次関数」のための基本勉強

なんですよね。

この形は中学３年生で学ぶ内容なのですが、

苦手としている人が多いです。

しかし看護受験では必ず出題されます。

この問題を

解けるのか？解けないのか？

でも、受験生の合否に大きくかかわってくるでしょう。

ですが、「二次関数」を勉強する前に、

この「二次方程式」のところで色々な知識を

頭の中に入れておく必要があります。

それでは、判別式の説明をしていきます。

判別式って何？

判別式でできることは、

簡単な計算で、

Xの解が何個出てくるのか？

調べることが出来ます。

前回も勉強しましたが、

３つのパターンがありましたよね？

・異なる２つの実数解
・重解
・実数解をもたない

この３点を最後まで計算しなくても、

判別式に入れてあげれば、

すぐにわかるんですよね。

ではどういうものが判別式なのか？

これを

判別式と言います。

どこかで見覚えがありませんか？

そうなんです。

解の公式のこの部分です。

ココさえ計算すれば、

・異なる２つの実数解
・重解
・実数解をもたない

どれなのかが、すぐにわかるんですよね。

その代わり条件はあります。

このように、

「0より大きい」「0と同じ」「0より小さい」

と判断できれば、

解の個数がわかります。

次回は、判別式を使って問題を解いてみましょう。

• vol.11：方程式と不等式 : 二次方程式の実数解の個数
• vol.13：方程式と不等式 : 判別式で解く問題はこれ！»

フォローして今すぐ看護受験情報をGET

日時間分秒

今回の数学のプチ授業は、

いよいよ高校数学本番って感じです。

何が？って思いますよね。

看護受験を目指して

数学を勉強している時には、

聞いたこともない日本語が

多々出てきます。

その日本語によって、

受験生のやる気を失わさせるんですよね。

そして、その１つが

実数解です。

今回はその実数解について説明していきます。

実数解って何？

「二次方程式と二次不等式」の勉強では、

常に、Xの答えが

２つ出ていませんでしたか？

いやいや、

１つの時もありませんでしたか？

では、少しおさらいをしてみましょう。

解くことができましたか？

答えは、

この場合のXの答え（実数解）は

１つですね。

では、もう一つ解いてみましょう。

できましたか？

どうやらこの問題の場合は、

Xの答え（実数解）が２つ

ありますよね？

このように、

この二次方程式を解いた場合には、

Xの答え（実数解）が２つ
or
Xの答え（実数解）が１つ

の時があります。

さらには、

計算した結果、まさかの

Xの答え（実数解）がない場合

もあります。

まとめてみると、

この３点は、必ず覚えておきましょう。

この知識は二次関数で必ず必要になってきます。

• vol.10：方程式と不等式 : 二次方程式と解の公式
• vol.12：方程式と不等式 : 判別式って何？»

フォローして今すぐ看護受験情報をGET

日時間分秒

皆様が二次方程式を解いていると

思わず、

これ因数分解ができないんだけど・・・

と、問題でぶつかる時があります。

では、因数分解が出来ない場合には

どうすればいいのでしょうか？

と、そこで利用するのが

解の公式です。

解の公式って何？

って思いましたか？

これは、中学3年生で学ぶ内容ですが、

公式を覚えておく必要があります。

それでは次の問題を解いてみてください。

できましたか？

もし、解の公式を忘れている場合は、

これを覚えていてください。

これは、何が何でも覚えておきたいです。

解の公式に関しては、

「正看護学校」でも「准看護学校」でも

どちらの学校でも必須です。

では、解説していきます。

なんとなく理解できましたか？

解の公式は

代入するときに、間違える学生が多いので

要チェックですね。

このように、因数分解が使えないときは、

頭の中をすぐに切り替え、

解の公式の利用をして下さい。

• vol.9：方程式と不等式 : 二次方程式の解き方
• vol.11：方程式と不等式 : 二次方程式の実数解の個数»

フォローして今すぐ看護受験情報をGET