
これまでの中学数学の復習、お疲れさまでした。
実は、「高校の2次関数」をしっかり理解するには、中学で学んだ内容がとても大切なんです。
それでは、ここから
高校数学の「2次関数」 に入っていきましょう!
2次関数の「𝑞」って何!?
突然、式の中にこんなのが出てくるとびっくりしますよね?
𝑦 = (𝑥 − 𝑝)² + 𝑞
この「𝑞」って何?
そう思った人も多いと思います。
実は中学数学の「𝑏」と同じなんです!
みなさん、1次関数の式
𝑦 = 𝑎𝑥 + 𝑏
は覚えていますか?
この中の「𝑏」は、
𝑦軸と交わる点(切片)を表していましたよね。
同じように、
2次関数の
𝑦 = 𝑎𝑥² + 𝑞
に出てくる 「𝑞」 も、
切片と同じく、グラフの位置を上下に動かす数字なんです。
つまり、「𝑞」はグラフの一番下(または上)の点の「𝑦座標」を表します。
では、実際に問題をやってみましょう!

まず、このグラフの一番下の点(頂点)はどこでしょうか?
式の形は、
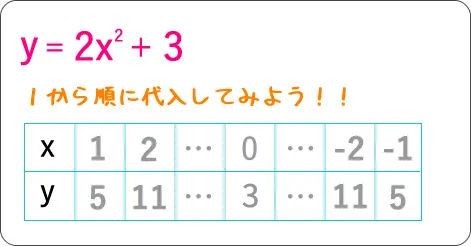
𝑦 = 2𝑥² + 3
なので、頂点は (0,3)
他にも「𝑥」に数字を代入して「𝑦」の値を書き出しておきましょう。
グラフの描き方
① まず、頂点(0, 3) に点を打ちます。
② 次に、先ほど「𝑥」と「𝑦」の点を増やします。
③ これらの点をなめらかな曲線でつなげば、完成です!
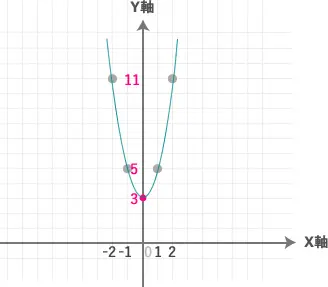
左右対称になっているのが分かりますね!
まとめ
✅ 「𝑞」は、グラフを上下に動かすための数字
✅ 頂点の𝑦座標を表す
✅ 式の形は、𝑦 = 𝑎𝑥² + 𝑞
◆ 看護受験の必須 二次関数を完璧に理解できる解説集 ◆
- Q1.2次関数とは
- Q2.グラフの見分け方のコツ
- Q3.グラフを書き方
- Q4.定義域・値域(1)
- Q5.定義域・値域(2)
- Q6.関数𝑓(𝑥)とは?
- Q7.上に凸と下に凸の見分け方。
- Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何?
- Q9.𝑦 = 𝑎(𝑥 - 𝑝)² の「𝑝」って何?
- Q10.𝑦 = 𝑎(𝑥 - 𝑝)² + 𝑞 :「𝑝 , 𝑞」は放物線の頂点。
- Q11.平方完成って何?
- Q12.平方完成の応用編
- Q13.放物線の平行移動①
- Q14.放物線の平行移動②
- Q15.象限って何?
- Q16.最大値・最小値って何?
- Q17.最大値と最小値の範囲を見極めよ①<
- Q18.最大値と最小値の範囲を見極めよ②
- Q19.軸に文字を含む場合の最大値と最小値①
- Q20.軸に文字を含む場合の最大値と最小値②
- Q21.軸に文字を含む場合の最大値と最小値③
- Q22.共有点の求め方
- Q23.判別式を使いこなそう。
- Q24.放物線とx軸が「異なる2点で交わる」問題。


































