
関数の勉強をしていると、こんな記号が出てくることがあります。
𝑓(𝑥)
初めて見た人は、
「えっ?なにこれ!?」って思いますよね。
でも大丈夫です!
これは、とっても便利な書き方なんです。
いつもこんなふうに書いていませんか?
たとえば、1次関数や2次関数の勉強のときに
・𝑥 = 1 のとき、𝑦 = 5
・𝑥 = 3 のとき、𝑦 = 8
こんなふうに書いたことありますよね?
でも毎回「𝑥 = □」って書くのって、正直ちょっと面倒くさいんです…。
そんな時に便利なのが「𝑓(𝑥)」
この「𝑓(𝑥)」という書き方は、
・「𝑥」に何を入れるか
・そのときの答えがいくつか
を、シンプルに表す方法なんです。
具体的に見てみましょう!
たとえば、このような関数があったとします。
𝑓(𝑥)=2𝑥+1
このとき、
「𝑥 に 1 を入れたときの値」は
𝑓(1)=2×1+1=3
となります。
つまり、
𝑓(1)=3
これは、
𝑥 = 1 のとき、𝑦 = 3
という意味と全く同じです。
もっとやってみよう!

この式を使って、いろんな値を代入してみましょう。
𝑓(𝑥)=2𝑥+1
𝑓(2)=2×2+1=5
𝑓(3)=2×3+1=7
𝑓(4)=2×4+1=9
このように、「𝑥」に好きな数字を入れるだけで、
答え(= 𝑦 の値)がすぐに出せます!
次の問題を解いてみましょう。

「𝑥」に4を代入して計算すればいいので、

できましたか?
これからは
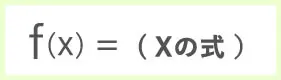
で書くことが増えるので覚えておきましょう。
ポイントまとめ
✅ 「𝑓(𝑥)」は「関数の式」の書き方
✅ 𝑓(1) は「𝑥 に 1 を入れたときの値」という意味
✅ 毎回「𝑥 = □、𝑦 = ○」と書かなくても、簡単に表せる
◆ 看護受験の必須 二次関数を完璧に理解できる解説集 ◆
- Q1.2次関数とは
- Q2.グラフの見分け方のコツ
- Q3.グラフを書き方
- Q4.定義域・値域(1)
- Q5.定義域・値域(2)
- Q6.関数𝑓(𝑥)とは?
- Q7.上に凸と下に凸の見分け方。
- Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何?
- Q9.𝑦 = 𝑎(𝑥 - 𝑝)² の「𝑝」って何?
- Q10.𝑦 = 𝑎(𝑥 - 𝑝)² + 𝑞 :「𝑝 , 𝑞」は放物線の頂点。
- Q11.平方完成って何?
- Q12.平方完成の応用編
- Q13.放物線の平行移動①
- Q14.放物線の平行移動②
- Q15.象限って何?
- Q16.最大値・最小値って何?
- Q17.最大値と最小値の範囲を見極めよ①<
- Q18.最大値と最小値の範囲を見極めよ②
- Q19.軸に文字を含む場合の最大値と最小値①
- Q20.軸に文字を含む場合の最大値と最小値②
- Q21.軸に文字を含む場合の最大値と最小値③
- Q22.共有点の求め方
- Q23.判別式を使いこなそう。
- Q24.放物線とx軸が「異なる2点で交わる」問題。


































