2次関数 : 定義域・値域（２）
「二次関数の値域には要注意の巻」vol.5

前回は、「一次関数の定義域と値域」について学びましたね。

今回は、その応用として 「二次関数の定義域と値域」 を学んでいきましょう。

まず問題を見てみましょう！

前にやったように、「𝑥」にいろいろな数字を代入して、

それぞれの「𝑦」の値を出していきます。

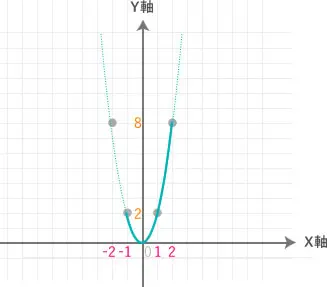
この表の5つの点をグラフに打って、曲線でつないでください。

2次関数のグラフは曲線（放物線）になりますよ！

定義域に注意！

問題では、「𝑥」の範囲が -1 から 2 の間 って言われていましたね。

だから、グラフはこの範囲だけを実線で描き、

それ以外の部分は点線や省略にして、書かないようにしましょう。

なので、「𝑥」の範囲以外の範囲は関係ないので、点線にしてあげます。

次は「値域」を見てみましょう！

値域とは、「𝑦」の値がどこからどこまで動くかです。

グラフを見るポイント：

一番下の「𝑦」の値 → 最小値
一番上の「𝑦」の値 → 最大値

表をもう一度見ると：

一番小さい「𝑦」の値 → 0（𝑥 = 0 のとき）
一番大きい「𝑦」の値 → 8（𝑥 = 2 のとき）

よくある間違いに注意！

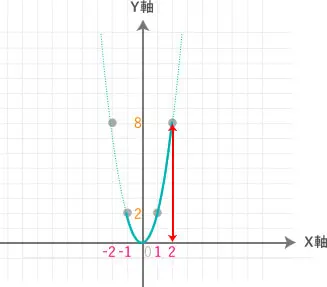
例えば、両端の 𝑥 = -1（𝑦=2）と 𝑥 = 2（𝑦=8）だけを見て
「2から8」と答えてしまう人がいますが、これは間違い！

一番小さい「𝑦」の値はどこか？
一番大きい「𝑦」の値はどこか？

この2つのポイントをしっかり見て判断する必要があります。

従って、下記のようなグラフになります。

ポイントまとめ

🔵 定義域は「𝑥の動く範囲」
🔴 値域は「𝑦の動く範囲（一番低いところから高いところまで）」

グラフを書くときは：

・「𝑥」の範囲を守って点を打つ
・曲線をきれいにつなぐ
・「𝑦」の最小値・最大値をしっかり見る

• «Q4.定義域・値域（1）
• Q6.関数f（𝑥）とは？»