2次関数 : 軸に文字を含む場合の最大値と最小値③
「高校数学：最大値の場合分けは範囲を半分で分けようの巻」vol.21

2次関数を勉強していると必ずと言っていいほど、

「最小値」や「最大値」が聞かれます。

前回は最小値の見つけ方を説明しましたが、

今回は「最大値」の見つけ方を説明していきます。

最大値を見つけたい時には範囲を半分に分けよう。

前回と今回の問題の違いは、

「最小値」なのか「最大値」なのか

この違いです。

最小値の場合はまだイメージがつくのですが、

最大値になると理解できない人が多いです。

というよりもやり方を知らない学生もたくさんいます。

では、前回同様、まずは左端の紫色の放物線から見ていきましょう。

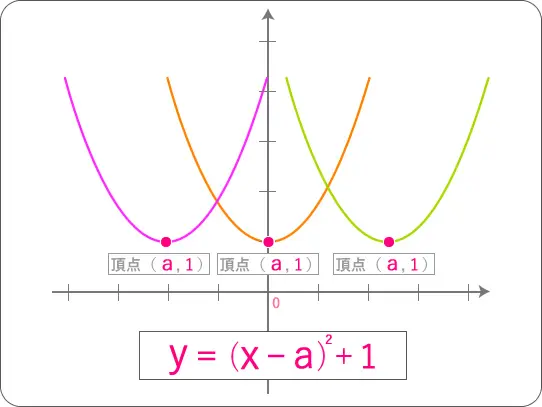
このような式の場合、解っていることは、

「放物線の向き」と「y = １」そして軸が「X ＝ a」

でしたよね。

ではこの左端の紫色の放物線に

(1≦x≦3)の範囲を与えたとするとどうなるのか！？

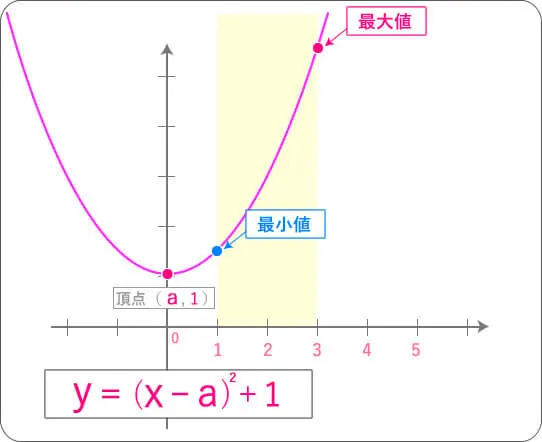
これを見るとどこが最大なのかわかりますね。

この場合はX＝３の時が最大だと言えます。

なので、

このようにしてあげると最大値が出てきます。

しかし、ここで

a≦2って何なの！？

と思いませんでしたか？

そうなんです。放物線の最大値を考えるときには、

範囲の真ん中（青い棒）を基準として考えます。

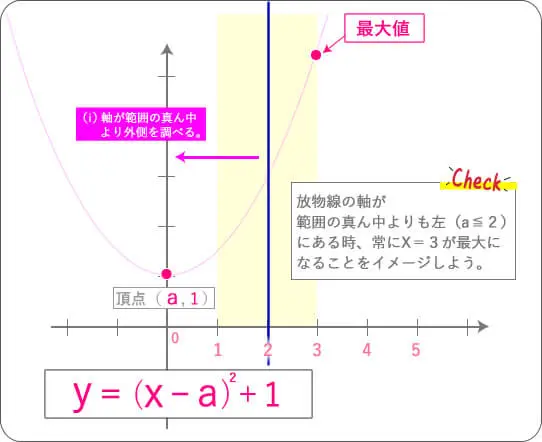
難しかったですよね。

これは一度読むだけでは理解できないかもしれませんので、

何度も読んでくださいね。

では、続いて、

右側の緑色の放物線を見てみましょう。

この場合の最大はどこになりますか？

そうです。

X=1の時に最大

になりますね。なので、

このようになります。

ここでも同じで、放物線の最大値を考えるときには、

範囲の真ん中（青い棒）を基準として考えます。

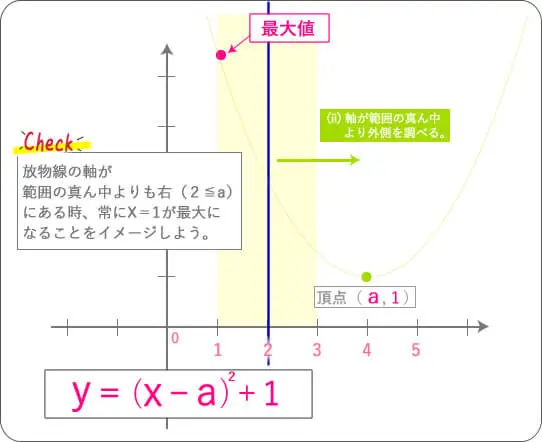
では最後にオレンジ色の放物線(1≦x≦3)にある場合ですね。

この場合はX=2に放物線を重ねてみます。

この場合は、最大値が2つ出てきます。

これも一応場合分けしておきます。

このように放物線の最大値は、

範囲の真ん中（青い棒）を基準に場合分けすることを心がけましょう。

• «Q20.軸に文字を含む場合の最大値と最小値②
• Q22.共有点の求め方»