2次関数 : 最大値と最小値の範囲を見極めよ②
「高校数学：変則的な範囲には気を付けての巻」vol.18

前回に続き、今回も

2次関数の「最大値」と「最小値」のお勉強をしていきましょう。

今回はもう一度復習も含めて説明していきたいと思います。

まず2次関数とは何なのか！？

最終的に

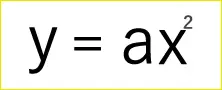
このような式の形になるものをいいます。

そして、

これをグラフにすれば

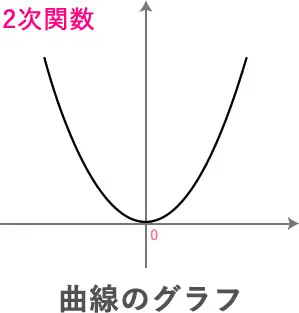
必ずこのような曲線のグラフになります。

ここまでは中学3年生までの内容です。

ここからは、

高校数学になりますが、

高校数学になるとこの曲線が、

原点（0,0）をとおるだけではなく、

色々な位置に移動します。

例えば、

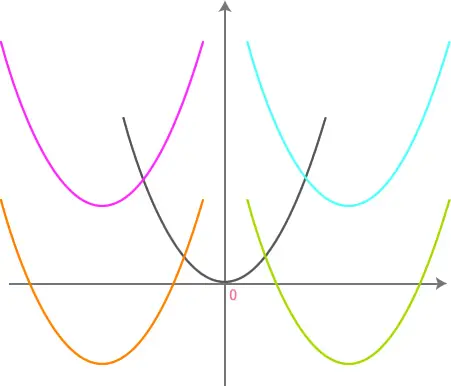
こんな感じで好き放題動いちゃうんです。

では、このように

好き放題動く放物線の式は！？

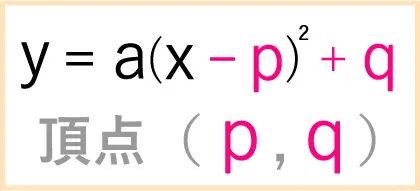
そうです。

これでしたよね。

この式の便利なところは、

上記にも書いてある通り、

頂点が解るところです。

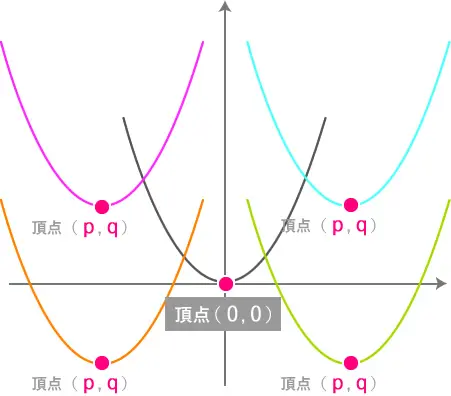
真ん中の放物線は、

原点を通っているので頂点は常に（0,0）

ですが、

あちこちに動いている放物線に関しては、

頂点の位置がわかりません。

なので、

「平方完成」というものを使い、

頂点を出してあげる必要があります。

なんとなく、

イメージ出来ましたか！？

それでは、本日のお題に戻りましょう。

頂点を含まない「最大値と最小値」の範囲には必ず座標を書こう。

それでは、早速問題を見てみましょう。

前回もお伝えしましたが、

目で見るのではなく

絶対に放物線を書こう。

でしたよね。

それでは、放物線を書いてみます。

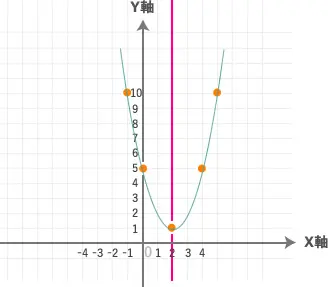
こんな感じの放物線ができましたか！？

このグラフの頂点はどこですか！？

（２,１）

次に軸はどこになりますか！？

X = 2

前回と同じですね。

それでは、今回の問題で聞いている範囲はどこでしょうか？

(4≦x≦5)の時の「最大値」と「最小値」

を聞いていますね。

それでは、この部分に色を塗ってみます。

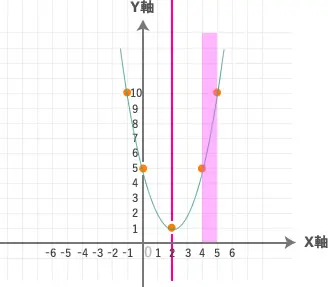
全く頂点は関係ありませんね。

重要なのは、

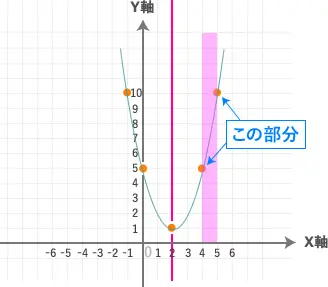
なので、この部分の座標を書きましょう。

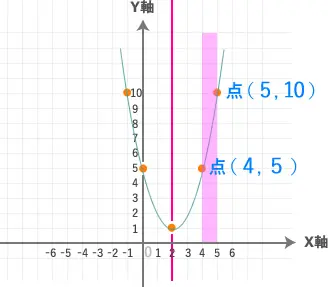
よって今回の

いつも頂点が「最小値」や「最大値」になるわけではないので、

気を付けて下さいね。

• «Q17.最大値と最小値の範囲を見極めよ①
• Q19.軸に文字を含む場合の最大値と最小値①»