2次関数 : 最大値・最小値って何？
「高校数学：下に凸と上に凸で異なるの巻」vol.16

まだ、2次関数が続くの！？

そう思ってしまうかもしれませんが、

2次関数はまだまだ続きます。

というよりも、

高校数学の数Ⅰは二次関数がメイン

と言ってもいいかもしれません。

そして、必ず看護学校の入試には出題されます。

まだまだ、

重要な項目を１つずつ小分けにして

説明していきますね。

それでは、

今回の2次関数で学ぶ「最小値と最大値」の説明をしていきます。

「最小値と最大値」はグラフの向きに要注意！！

まずはグラフを見てみましょう。

二次関数のグラフは必ず、

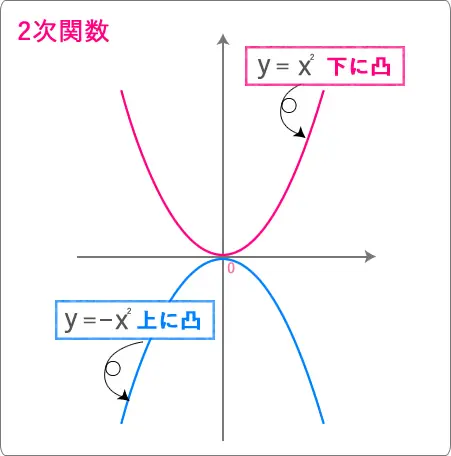
このようになっていますよね。

今回のお題にある「最小値」と「最大値」は

グラフの向きによって変わってきます。

例えば、下に凸のグラフであれば、

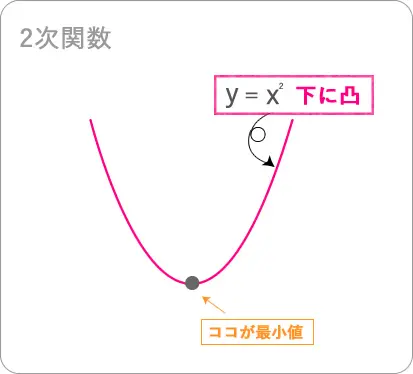
この部分が最小値になりますよね。

続いて、

上に凸であれば、

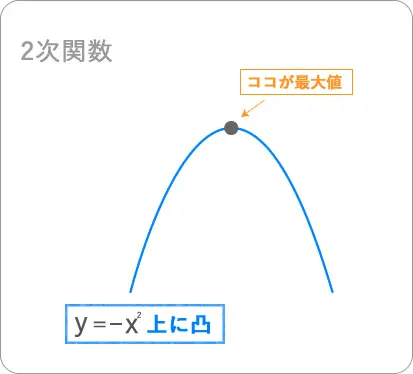
この部分が最大値になります。

と、ここで何が言いたいのかと言えば、

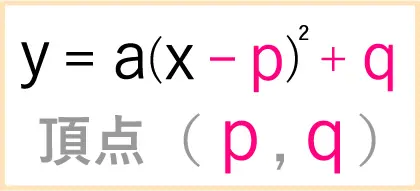
この「平方完成」で解いた頂点が

そのまま「最小値」「最大値」になる

ということです。

それでは例題を解いてみましょう。

まず解く前に重要なことは

見極めてください。ちなみに

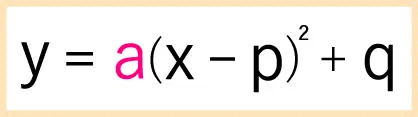
このaの部分が

+（プラス）なら下に凸
－（マイナス）なら上に凸

になります。

ということは、今回の問題は

＋（プラス）なので下に凸のグラフです。

下に凸ということが分かったので、

頂点（２,１）が最小値

になります。

• «Q15.象限って何？
• Q17.最大値と最小値の範囲を見極めよ①»