2次関数 : 平方完成って何？
「高校数学：平方完成があっという間に出来上がりの巻」vol.11

今回のテーマは「平方完成」です。

その前に、まだ2次関数が「苦手かも…」と感じている方は、
これまでの内容をもう一度読み返してみてくださいね。

「平方完成」って何？

今回のテーマは、初めて聞く方も多いかもしれません。
それが「平方完成（へいほうかんせい）」です！

平方完成って何をするの？

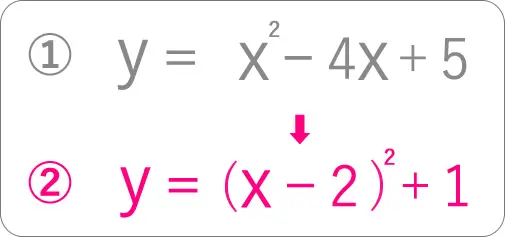
簡単に言うと、

という式を、

のように書きかえることです。

こうすることで、グラフの頂点を簡単に見つけられるようになります。

では、どうやって①の式を②の形に変えるのでしょうか？

平方完成のカギは「÷2」

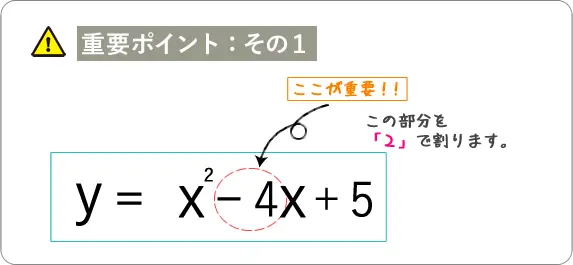
それでは実際にやってみましょう。

ステップ①：「𝑥の係数（-4）を2で割る」

-4 ÷ 2 = -2
この「-2」を使って、次のように書きかえます。

ステップ②：「余分に足した分を引いて調整する」

最終的には、

と同じ式になる必要があります。

さきほど作った (𝑥 – 2)² を展開すると、

となり、「+1」が足りないことがわかります。

ですので、

に「+1」を足してあげましょう。

補足

実はこの平方完成は、

中学3年生で学んだ因数分解がとても重要です。

因数分解に不安がある方は、

こちらのページで復習してみてくださいね。

まとめ：平方完成の手順

① 式が 𝑦 = 𝑥² – 𝑏𝑥 + 𝑐 の形になっているか確認する
② 𝑏 ÷ 2 を計算し、その数を使って (𝑥 ± 𝑏/2)² の形を作る
③ 展開して、元の式に合わせるように足りない（または余分な）数を調整する

• «Q10.「𝑝」と「𝑞」は放物線の頂点。
• Q12.平方完成の応用編»