
看護受験生にとって、
2次関数は一つの壁ですが、
看護受験には絶対に必要な部分なので、
ここから読んでいけば、
必ず理解できます。
今回から読み始めた人は
復習をしてからこの記事を読むと理解しやすいです。
また当看護予備校に通っている学生様は
記事の内容も質問OKなので、
何でも聞いてくださいね。
それでは、今回のお題の説明をしていきます。
2次関数の「最大値と最小値」の範囲を見極めよう!!
2次関数では必ずと言っていいほど、
「最大値」や「最小値」
が問われます。
では、それを見極めるにはどうすればいいのか!?
これは、目で見るだけでは無理です。
絶対に放物線を書いて下さい。
それでは、早速問題を解いてみましょう。

まずこの問題を見た時に
このグラフの頂点はどこですか!?
(2,1)
ですね。これは平方完成のところで勉強しました。
次に軸はどこになりますか!?
もちろん
X = 2
ですよね。
この時点で何を言ってるの!?と思った方は
しつこいようですが、
こちらから順に見て下さい。
では、グラフを書いてみましょう。
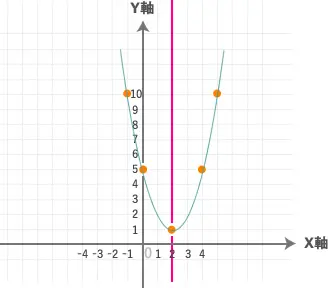
このようなグラフになりましたか!?
それでは今回の問題ですが、
(-1≦x≦4)の時の「最大値」と「最小値」
を聞いていますね。
では、(-1≦x≦4)の範囲に色を塗ってみます。
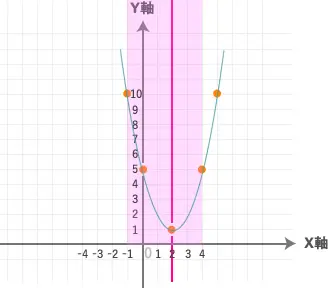
この紫色の部分が
(-1≦x≦4)の範囲
になります。
要するにこれ以外は考えなくていいんです。
では、この中でyの最大値と最小値はどこですか?
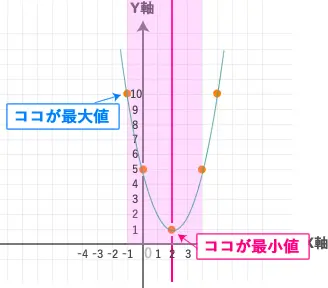
放物線を書いて色を塗るとわかりやすいですね。
よって今回の
最小値は「1」となります。
2次関数の「最大値と最小値」の問題も
看護学校の受験ではよく出題されるので、
要注意です。是非覚えておいて下さい。
◆ 看護受験の必須 二次関数を完璧に理解できる解説集 ◆
- Q1.2次関数とは
- Q2.グラフの見分け方のコツ
- Q3.グラフを書き方
- Q4.定義域・値域(1)
- Q5.定義域・値域(2)
- Q6.関数𝑓(𝑥)とは?
- Q7.上に凸と下に凸の見分け方。
- Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何?
- Q9.𝑦 = 𝑎(𝑥 - 𝑝)² の「𝑝」って何?
- Q10.𝑦 = 𝑎(𝑥 - 𝑝)² + 𝑞 :「𝑝 , 𝑞」は放物線の頂点。
- Q11.平方完成って何?
- Q12.平方完成の応用編
- Q13.放物線の平行移動①
- Q14.放物線の平行移動②
- Q15.象限って何?
- Q16.最大値・最小値って何?
- Q17.最大値と最小値の範囲を見極めよ①<
- Q18.最大値と最小値の範囲を見極めよ②
- Q19.軸に文字を含む場合の最大値と最小値①
- Q20.軸に文字を含む場合の最大値と最小値②
- Q21.軸に文字を含む場合の最大値と最小値③
- Q22.共有点の求め方
- Q23.判別式を使いこなそう。
- Q24.放物線とx軸が「異なる2点で交わる」問題。




































