
そろそろ看護学校の入試に向けて、
本腰が入ってきた頃ですか!?
でも、この時期は変化の伴う時期でもあります。
例えば、
高校生:進学の悩みやクラブ活動での重責
主婦:お子さんの新生活のスタート
色々なものが重なり、
ちょっとやる気が下がることもあります。
でも、こんな時こそ看護受験に向けて
何に注意するべきなのか!?
それは、
「毎日決めたページ数をやり続ける」
これが何よりも重要です。
4月、5月が終われば、「社会人入試」や「公募入試」がすぐやってきます。
当看護予備校の学生様は、
不安なことがあればいつでも問いかけて下さいね。
また、これから入学を考えている学生様も
無料体験&個別面談からお申し込み下さい。
それでは、本日も
2次関数の平行移動の続きを勉強していきます。
放物線の平行移動は平方完成が基本。
早速ではありますが、今回も問題を見てみましょう。

なんか難しそうな雰囲気ですよね。
ちなみに、これ
看護受験で出題される可能性
がかなり高い問題です。
では、どうすれば解けるのか!?
まず、
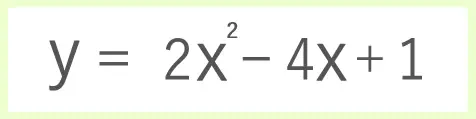
まず問題にこのような二次関数の式があれば、
躊躇なく平方完成
をして下さい。

ちなみに、平方完成のやり方は覚えていますか!?
もし忘れていたり、見逃した人は
こちらを見て下さいね。
平方完成が出来ましたね。
ということは、
この
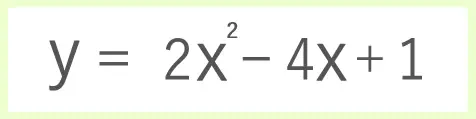
の放物線の頂点は、
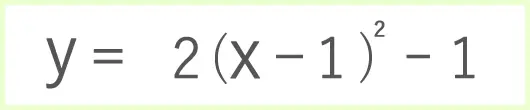
なので、
(1,-1)
と言えます。
で、今回この問題で聞いているは、
と言っているので、

このピンクの部分だけを書き換えてあげます。
これで、
放物線の式は完成しました。
実はもう少し簡単な考え方もあるのですが、
放物線の移動は、
常に平方完成を意識した方がいい
ので、二次関数の式を見れば、
すぐに平方完成にする癖をつけておきましょう。
◆ 看護受験の必須 二次関数を完璧に理解できる解説集 ◆
- Q1.2次関数とは
- Q2.グラフの見分け方のコツ
- Q3.グラフを書き方
- Q4.定義域・値域(1)
- Q5.定義域・値域(2)
- Q6.関数𝑓(𝑥)とは?
- Q7.上に凸と下に凸の見分け方。
- Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何?
- Q9.𝑦 = 𝑎(𝑥 - 𝑝)² の「𝑝」って何?
- Q10.𝑦 = 𝑎(𝑥 - 𝑝)² + 𝑞 :「𝑝 , 𝑞」は放物線の頂点。
- Q11.平方完成って何?
- Q12.平方完成の応用編
- Q13.放物線の平行移動①
- Q14.放物線の平行移動②
- Q15.象限って何?
- Q16.最大値・最小値って何?
- Q17.最大値と最小値の範囲を見極めよ①<
- Q18.最大値と最小値の範囲を見極めよ②
- Q19.軸に文字を含む場合の最大値と最小値①
- Q20.軸に文字を含む場合の最大値と最小値②
- Q21.軸に文字を含む場合の最大値と最小値③
- Q22.共有点の求め方
- Q23.判別式を使いこなそう。
- Q24.放物線とx軸が「異なる2点で交わる」問題。


































