
前回の
平方完成は理解できましたか!?
数学はちょっとしたコツがわかれば
解ける問題も多いんです。
もちろん、因数分解もすごく大切なので、
できる限り基礎は大切して下さいね。
それでは、今回は
「平方完成の応用」を説明していきます。
平方完成の応用はこの部分に注意。
前回学んだ、
平方完成を簡単にするコツは

この式の
灰色の部分を覚えておくこと
でしたね。
では、
こんな式の場合はどうなりますか?
1つ例題を解いてみましょう。
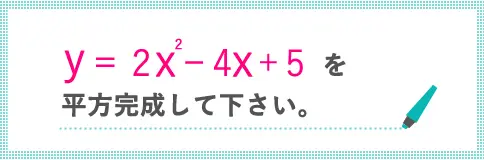
えっ・・・
Xの2乗の前に数字があるけど???
なんて思いましたか?
そうなんです。
ここで注意点があります。
このままでは平方完成はできません。

では、
どうすればいいのか!?
Xの2乗の前についている数字
これをカッコでくくりましょう。

できましたか?
こうすることにより、
前回やった問題と同じパターンになりましたね。
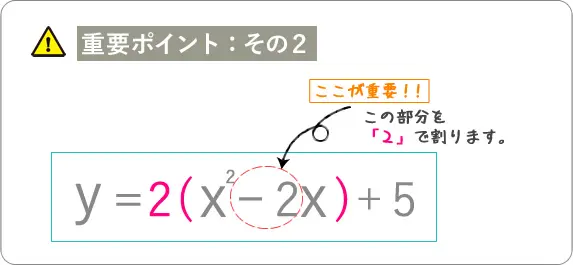
それでは、いつも通りこの部分を
「÷2」
をして下さいね。
すると答えは
「-1」
になりましたね。
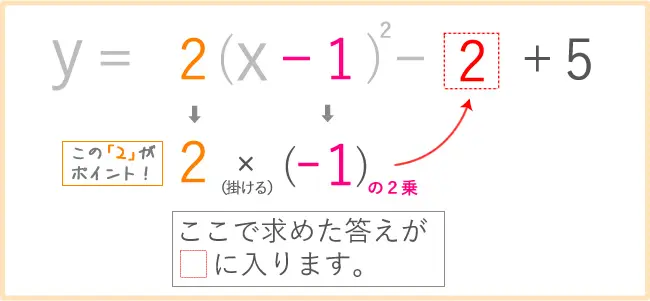
では、式を書いてみます。

同じようになりましたか!?
では、
最後に赤い□に答えを書きたいところですが、
もう一つ注意点があります。
それは、
オレンジ色の2の部分を忘れないこと
です。
ちょっと難しかったですか?
数学は、
たった1つ別の行動が増えるだけで
ややこしくなります。
でも、何度か見返していると
「ピーンっと閃くとき」
が来るので、
少し我慢して読み返して下さいね。
後は、「-2」と「5」を計算して終了です。
これで
平方完成の出来上がりです。
これさえできれば、
平方完成はお手の物です。

後は、解けば解くほど慣れるので、
平方完成を自分のもとして下さい。
◆ 看護受験の必須 二次関数を完璧に理解できる解説集 ◆
- Q1.2次関数とは
- Q2.グラフの見分け方のコツ
- Q3.グラフを書き方
- Q4.定義域・値域(1)
- Q5.定義域・値域(2)
- Q6.関数𝑓(𝑥)とは?
- Q7.上に凸と下に凸の見分け方。
- Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何?
- Q9.𝑦 = 𝑎(𝑥 - 𝑝)² の「𝑝」って何?
- Q10.𝑦 = 𝑎(𝑥 - 𝑝)² + 𝑞 :「𝑝 , 𝑞」は放物線の頂点。
- Q11.平方完成って何?
- Q12.平方完成の応用編
- Q13.放物線の平行移動①
- Q14.放物線の平行移動②
- Q15.象限って何?
- Q16.最大値・最小値って何?
- Q17.最大値と最小値の範囲を見極めよ①<
- Q18.最大値と最小値の範囲を見極めよ②
- Q19.軸に文字を含む場合の最大値と最小値①
- Q20.軸に文字を含む場合の最大値と最小値②
- Q21.軸に文字を含む場合の最大値と最小値③
- Q22.共有点の求め方
- Q23.判別式を使いこなそう。
- Q24.放物線とx軸が「異なる2点で交わる」問題。


































