2次関数 : 上に凸と下に凸の見分け方。
「一箇所見ればすぐにわかるの巻」vol.7

二次関数のグラフには「上開き」 と 「下開き」の2パターンがあります。

これらは、式の中にある符号によって異なるので詳しく見ていきましょう。

式を見て、どこが違うか探してみよう！

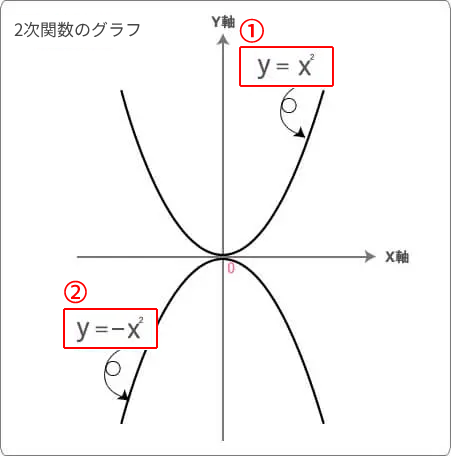
上記のグラフの式は

① 𝑦 = 𝑥²
② 𝑦 = −𝑥²

です。

では、この2つのどこが違うか分かりますか？

違いはここ！

①の式は、「𝑦 = 𝑥²」
②の式は、「𝑦 = −𝑥²」

2つ式の違いは、「𝑥²」の前にマイナス（−）がついているかいないかです。

この符号が、グラフの向き（形）を決めるカギなんです！

符号とグラフの向きの関係

「𝑥²」の前の符号が

プラス（＋）の時、下に凸（したにとつ）
マイナス（−）の時、上に凸（うえにとつ）

になります。

「開く向き」と「凸（とつ）」は逆の方向になるので、要注意です。

まとめ

✅ 二次関数の式を見ると、グラフの「向き」が分かる！
✅ 「𝑥²」の前の符号が「＋」か「−」かをチェックしよう！
✅ 「上に開く」は 下に凸、「下に開く」は 上に凸 と言います！

• «Q6.関数𝑓(𝑥)とは？
• Q8.𝑦 = 𝑎𝑥² + 𝑞 の「𝑞」って何？»