2次関数 : 軸に文字を含む場合の最大値と最小値①
「高校数学：文字に騙されないようにしようの巻」vol.19

本日よりいよいよ「令和」の幕開けですね。

ゴールデンウイークはいかがお過ごしですか！？

雨が続いているのが残念ですよね。

こういった長期の休みは

いつものルーティンワークが崩れたりします。

休みなのに休み明けに全く勉強ができていなかった・・・

なんてよくあるんですよね。

だからこそ、いつも通り問題集を進めることが

重要です。

それでは、またまた２次関数の説明をしていきます。

軸に文字を含む放物線の動きを覚えておこう。

「文字」

これによって

人の頭脳が働かなくなります。

今回学習する範囲は、

2次関数の中でも一番難しい内容かもしれません。

なので、今回は２回に分けて説明していきます。

今回は、放物線がどのように移動するのか！？

それだけを勉強しましょう。それでは問題を見て下さい。

文字が入っている・・・

何これ！？難しい・・・

とリアクションをとって頂いて大丈夫です。

確かに、式に文字が含まれているのですが、

前まで見ていた式と同じですよね。

では、１つずつ紐解いていく行きましょう。

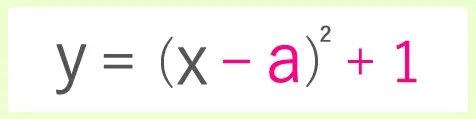
放物線の式だけを取り出してみました。

ここで重要なのは、どれだけ難しい問題が出てきたとしても、

①　軸
②　頂点
③　放物線の向き

これだけは前もって準備しなければなりません。

では一緒にやってみましょう。

まず、

X=a

ですよね。

続いて

（a , 1）

最後に

下に凸
ですよね。

では放物線を書いてみたいと思います。

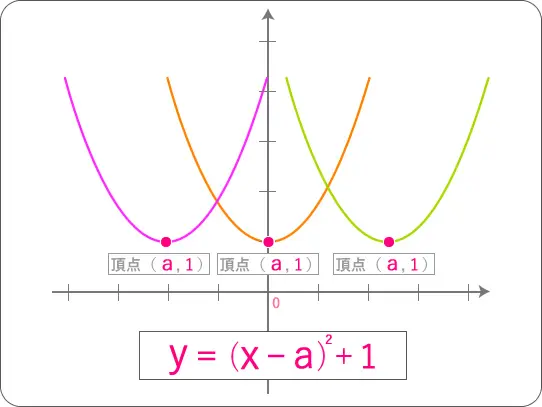
現時点で解っていることは、

「放物線の向き」と「y = １」そして軸が「X ＝ a」

ですよね。

なので、放物線が右に左にとフラフラしている状態です。

明日は、このフラフラしている放物線が

(1≦x≦3)の間であればどのような動きになるのかを

説明します。

• «Q18.最大値と最小値の範囲を見極めよ②
• Q20.軸に文字を含む場合の最大値と最小値②»