日
時間
分
秒
本日も看護受験に必須の数学の公式を極めていきましょう。
連立一次不等式の応用
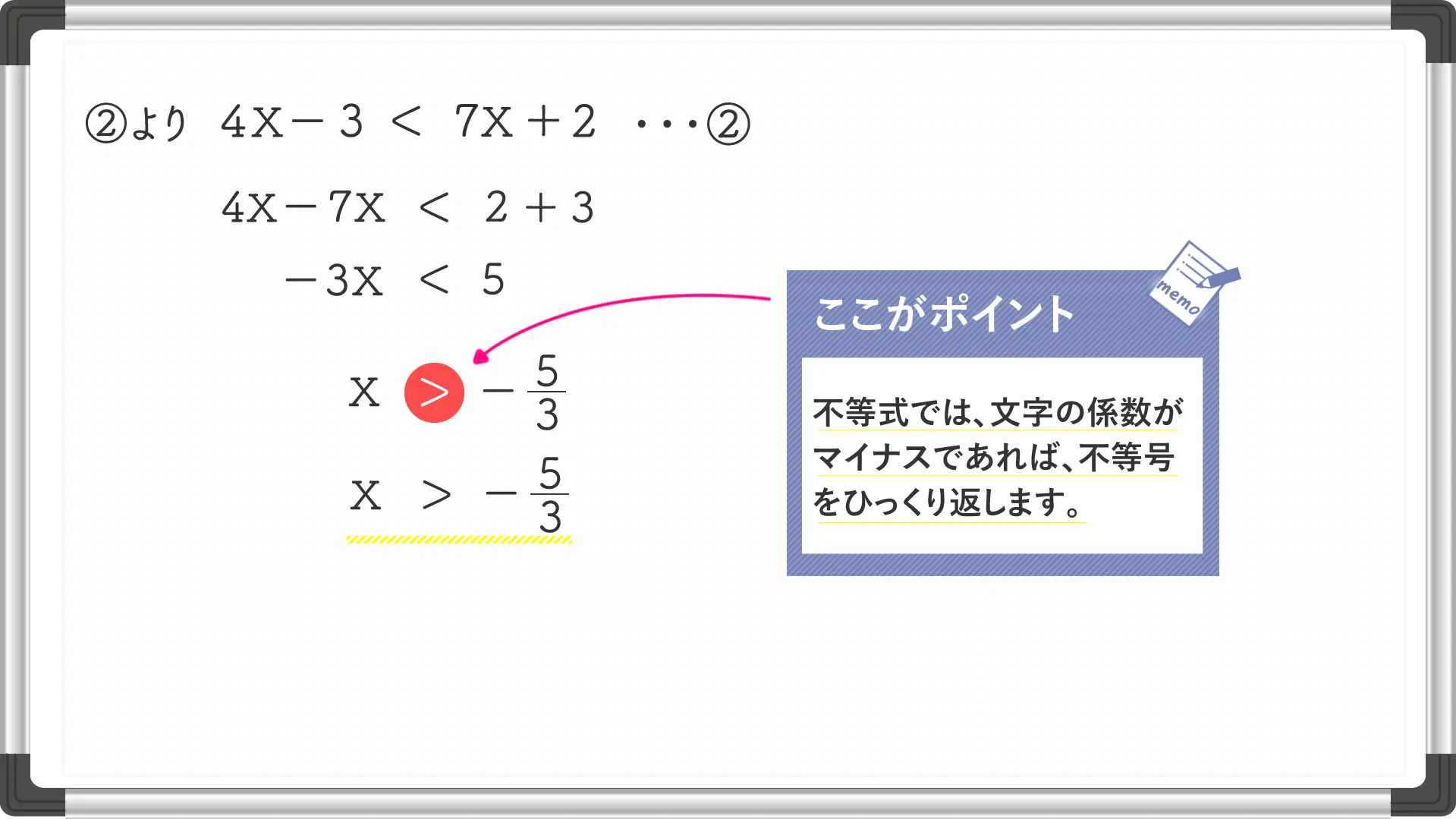
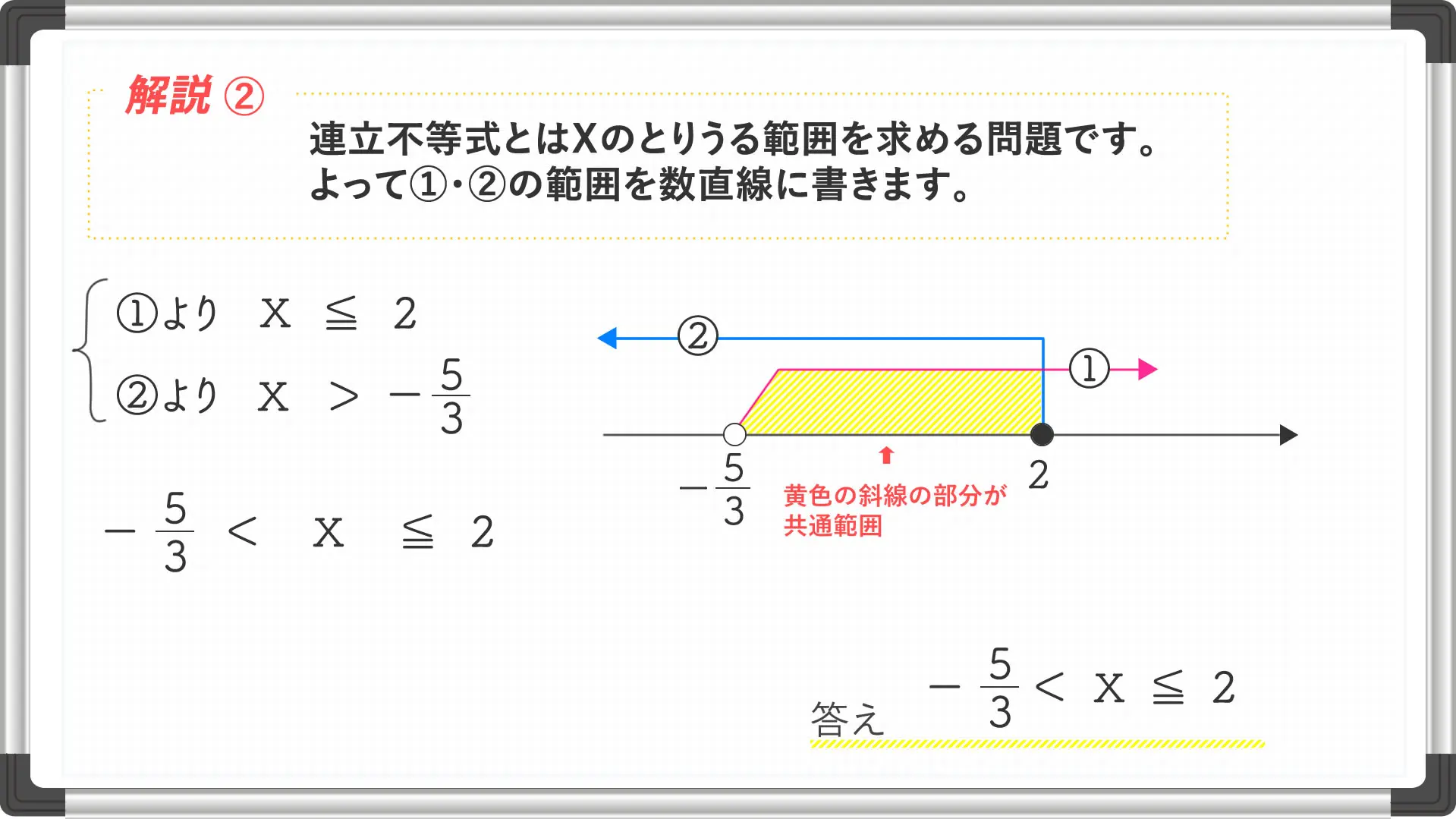
連立一次不等式の問題では、初めから連立として書いている場合と
今回の問題のように横並びになっている問題があります。
横並びなっている不等式の場合は、連立に書き直してから
解くことで間違いが減少します。
◆ 看護受験の必須 受験前には確認しておきたい数学公式問題集 ◆
- Q1.乗法の公式（1）
- Q2.乗法の公式（2）
- Q3.乗法の公式（3）
- Q4.乗法の公式（4）
- Q5.因数分解の公式（1）
- Q6.因数分解の公式（2）
- Q7.因数分解の公式（3）
- Q8.絶対値の基本
- Q9.平方根の基本
- Q10.平方根の応用
- Q11.根号（√）ルートの基本
- Q12.有理化の分数計算
- Q13.２重根号の解き方
- Q14.２重根号の応用
- Q15.一次方程式と一次不等式の違い
- Q16.一次不等式の応用
- Q17.連立1次不等式の解き方
- Q18.連立1次不等式の応用
- Q19.絶対値と不等式の基本
- Q20.集合の表し方
- Q21.二次関数の公式
- Q22.暗記だけで二次関数の頂点を求める方法
- Q23.頂点の平行移動が公式だけすぐにわかる方法
- Q24.頂点の対象移動の仕組み。
- Q25.定義域に制限がある場合の最大と最小
- Q26.二次方程式と因数分解
- Q27.判別式（異なる２点で交わる実数解）
- Q28.判別式（重解をもつ）
- Q29.判別式（解をもたない問題）
- Q30.三角比（sinサインの読み方）
- Q31.三角比（cosサインの読み方）
- Q32.三角比（tanタンジェントの読み方）
- Q33.正弦(sin)と余弦(cos)の公式を利用した計算
- Q34.正接(tan)の公式を利用した計算
- Q35.正弦(sin)と余弦(cos)と正接(tan)の復習
- Q36.sin(90°−θ)とcos(90°−θ)の覚え方
- Q37.tan(90°−θ)の覚え方
- Q38.sin,cos,tan(180°−θ)の覚え方
- Q39.正弦定理について
- Q40.余弦定理について
看護 予備校 KAZアカデミーが作成。看護受験に役に立つ学習一覧
